题目内容
(2012•淄博二模)点P(2,-1)为圆(x-3)2+y2=25的弦的中点,则该弦所在直线的方程是
x+y-1=0
x+y-1=0
.分析:由圆的方程找出圆心A的坐标,再由P的坐标,求出直线AP的斜率,由P为弦的中点,根据垂径定理得到过P的直径与弦垂直,利用两直线垂直时斜率的乘积为-1,得出弦所在直线的斜率,最后由P的坐标和求出的斜率,写出弦所在直线的方程即可.
解答:解:由圆的方程得到圆心A坐标为(3,0),
又P(2,-1),∴直线AP的斜率为
=1,
由P为弦的中点,得到过P的直径与该弦垂直,
∴该弦所在直线方程的斜率为-1,
则弦所在直线的方程为:y-(-1)=-(x-2),即x+y-1=0.
故答案为:x+y-1=0
又P(2,-1),∴直线AP的斜率为
| 3-2 |
| 0-(-1) |
由P为弦的中点,得到过P的直径与该弦垂直,
∴该弦所在直线方程的斜率为-1,
则弦所在直线的方程为:y-(-1)=-(x-2),即x+y-1=0.
故答案为:x+y-1=0
点评:此题考查了直线与圆相交的性质,涉及的知识有:垂径定理,两直线垂直时斜率满足的关系,以及直线的斜截式方程,根据P为弦的中点,利用垂径定理得:过P的直径与弦垂直是本题的突破点.

练习册系列答案
相关题目
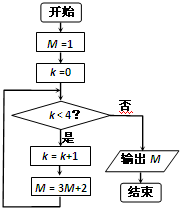 (2012•淄博二模)执行如图所示的程序框图,输出的M的值为( )
(2012•淄博二模)执行如图所示的程序框图,输出的M的值为( )