题目内容
（2012•淄博二模）△ABC中，∠C=90°，且CA=CB=3，点M满足
=2
，则
•
=（ ）
| BM |
| AM |
| CM |
| CA |
分析：由题意可得△ABC是等腰直角三角形，AB=3
，
=
，把要求的式子化为9+（
-
）•
，再由两个向量垂直的性质运算求得结果．
| 2 |
| AM |
| BA |
| CA |
| CB |
| CA |
解答：解：由题意可得△ABC是等腰直角三角形，AB=3
，
=
，故
•
=（
+
）•
=
2+
•
=9+
•
=9+（
-
）•
=9+
2-
•
=9+9-0=18，
故选A．
| 2 |
| AM |
| BA |
| CM |
| CA |
| CA |
| AM |
| CA |
| CA |
| AM |
| CA |
| BA |
| CA |
=9+（
| CA |
| CB |
| CA |
| CA |
| CB |
| CA |
故选A．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量垂直的性质，属于基础题．
练习册系列答案
相关题目
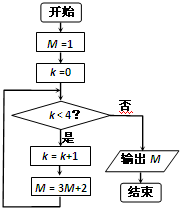（2012•淄博二模）执行如图所示的程序框图，输出的M的值为（ ）