题目内容
20．△ABC中，若A=60°，$a=\sqrt{3}$，则$\frac{a+b}{sinA+sinB}$=2．分析 由已知利用比例的性质，正弦定理即可计算得解．
解答 解：∵A=60°，$a=\sqrt{3}$，
∴$\frac{a+b}{sinA+sinB}$=$\frac{a}{sinA}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2．
故答案为：2．
点评 本题主要考查了比例的性质，正弦定理的应用，属于基础题．
练习册系列答案
相关题目
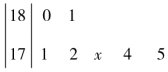某校文科班7名男生身高（单位：厘米）分布的茎叶图如图，已知7名男生的平均身高为175cm，但有一名男生的身高不清楚，只知道其末位数为x，那么x的值为2．