题目内容

2．复数z=1+i，z、i所对应的点为A、B，O是坐标原点，则三角形AOB的面积为$\frac{1}{2}$．

分析 求出复数对应点的坐标，结合图形，即可得到结论．

解答 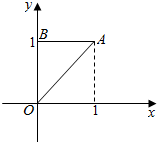解：根据复数的几何意义知A（1，1），B（0，1），
如图所示；
则三角形OAB的面积为S=$\frac{1}{2}$×1×1=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．

点评 本题考查了三角形面积的计算问题，利用复数的几何意义求出A，B的坐标是解决本题的关键．

练习册系列答案
相关题目
12．过抛物线y2=2px（p＞0）的焦点F，引两条相互垂直的弦AC，BD．求四边形ABCD面积的最小值为8p2．
13．若x＞$\frac{2}{3}$，则y=x+$\frac{4}{3x-2}$的最小值是$\frac{4\sqrt{3}}{3}$
若x＜2，则y=$\frac{5-4x+{x}^{2}}{2-x}$的最小值是2．
10．已知数列{an}满足a1=1，an+1=$\frac{{a}_{n}}{1+{{a}_{n}}^{2}}$（n∈N*）．
（1）证明：当n≥1，n∈N*时，$\frac{2}{n+2}$≤an≤1；
（2）设Sn为数列{an}的前n项和，证明：Sn≤$\sqrt{2n-1}$（n∈N*）．
17．直线l的方向向量为（sinθ，cosθ），θ∈（-$\frac{π}{2}$，0），则l的倾斜角为（　　）
A．π-θB．$\frac{π}{2}$+θC．$\frac{π}{2}$-θD．θ
7．在平面直角坐标系中，点P（1，2cos2A）和Q（sin2A，-1）分别在角α、角β的终边上，且$\overrightarrow{OP}$•$\overrightarrow{OQ}$=$\frac{1}{4}$，已知锐角△ABC的内角A，B，C的对边分别为a，b，c．
（1）求tan（α+β）；
（2）若a=3，求BC边上的高的最大值．
14．集合M={m|m=3n，n∈N且100＜m＜1000}的元素个数为300．
11．log34•log48•log87•log7m=log39，那么m=（　　）
A．27B．18C．9D．$\frac{9}{2}$
1．命题p：?x∈R，ax2+ax+1＞0，若?p是真命题，则实数a的取值范围是（　　）
A．（0，4]B．[0，4]C．（-∞，0）∪[4，+∞）D．（-∞，0）∪（4，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网