题目内容
 利用校园内围墙一角和篱笆围成一个面积为128m2的直角梯形花园,已知两围墙所成角为135°(如图),则所用篱笆总长度的最小值为( )
利用校园内围墙一角和篱笆围成一个面积为128m2的直角梯形花园,已知两围墙所成角为135°(如图),则所用篱笆总长度的最小值为( )A、16
| ||
| B、32m | ||
| C、64m | ||
| D、16m |
考点:基本不等式在最值问题中的应用
专题:计算题,不等式的解法及应用
分析:先设出BD=x,篱笆长度为y,进而分别表示出CD,AB,进而根据梯形面积公式建立等式,表示出y,利用基本不等式求得y的最小值.
解答:
 解:如图,设BD=x,设篱笆长度为y,则CD=y-x,AB=y-2x,
解:如图,设BD=x,设篱笆长度为y,则CD=y-x,AB=y-2x,
梯形的面积为
=128,
整理得y=
+
≥16
,当
=
x等号成立,
所以篱笆总长度最小为16
m.
故选:A.
 解:如图,设BD=x,设篱笆长度为y,则CD=y-x,AB=y-2x,
解:如图,设BD=x,设篱笆长度为y,则CD=y-x,AB=y-2x,梯形的面积为
| (y-2x+y-x)•x |
| 2 |
整理得y=
| 128 |
| x |
| 3x |
| 2 |
| 3 |
| 128 |
| x |
| 3 |
| 2 |
所以篱笆总长度最小为16
| 3 |
故选:A.
点评:本题主要考查了基本不等式的应用.解题的关键是根据题意建立数学模型.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
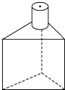
下列选项中不是右图中几何体的三种视图之一的是( )

A、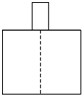 |
B、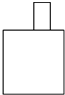 |
C、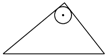 |
D、 |
已知{an}是由正数组成的数列,其前n项和Sn与an之间满足:an+
=
(n≥1且n∈N*).
(Ⅰ)求数列{an}的通项an;
(Ⅱ)设bn=(
)nan,求数列{bn}的前n项和Tn.
| 1 |
| 2 |
2Sn+
|
(Ⅰ)求数列{an}的通项an;
(Ⅱ)设bn=(
| 1 |
| 2 |
点(x,y)的坐标x,y都是有理数时,该点称为有理点,在半径为r,圆心为(a,b)的圆中,若a∈Q,b∈Q,则这个圆上的有理点的数目为( )
| A、最多有一个 |
| B、最多有两个 |
| C、最多有三个 |
| D、可以有无穷多个 |
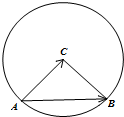 如图,定圆C半径为r,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且
如图,定圆C半径为r,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且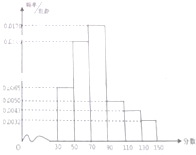 某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图:
某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图: