题目内容
11.在△ABC中,角A,B,C的对边分别为a,b,c,A=$\frac{3π}{4}$,cosB=$\frac{3\sqrt{10}}{10}$,AD为BC边上的中线,且AD=1.(1)求sinC的值;
(2)求△ABC的面积.
分析 (1)求得sinB,根据三角形中sinC=sin(A+B),利用两角和的正弦公式,展开求得sinC;
(2)设BD=CD=x,AC=y,由正弦定理求得x与y的关系,由余弦定理,1=${y}^{2}+{x}^{2}-2xy•\frac{2\sqrt{5}}{5}$,代入,求得x,y的值,再由三角形面积公式求得其面积.
解答 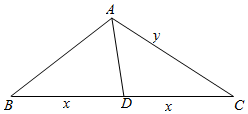 解:(1)在△ABC中,cosB=$\frac{3\sqrt{10}}{10}$,sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{\sqrt{10}}{10}$,
解:(1)在△ABC中,cosB=$\frac{3\sqrt{10}}{10}$,sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{\sqrt{10}}{10}$,
sinC=sin[π-(A+B)]=sin(A+B)=sinAcosB+cosAsinB,
∴sinC=$\frac{\sqrt{2}}{2}$•$\frac{3\sqrt{10}}{10}$+(-$\frac{\sqrt{2}}{2}$)•$\frac{\sqrt{10}}{10}$,
=$\frac{\sqrt{5}}{5}$,
cosC=$\frac{2\sqrt{5}}{5}$,
(2)设BD=CD=x,AC=y,
在三角形ABC中,由正弦定理得:$\frac{AC}{sinB}=\frac{BC}{sinA}$,
得:$\frac{y}{\frac{\sqrt{10}}{10}}=\frac{2x}{\frac{\sqrt{2}}{2}}$,
∴y=$\frac{2\sqrt{5}}{5}x$,在△ACD中,由余弦定理:AD2=AC2+CD2-2AC•CDcosC,
∵A=$\frac{3π}{4}$,0<C<$\frac{π}{4}$,
cosC=$\frac{2\sqrt{5}}{5}$,
∴1=${y}^{2}+{x}^{2}-2xy•\frac{2\sqrt{5}}{5}$,
解得:$\left\{\begin{array}{l}{x=\sqrt{5}}\\{y=2}\end{array}\right.$,
∴S△ABC=$\frac{1}{2}$AC•BC•sinC=$\frac{1}{2}$×2×2$\sqrt{5}$×$\frac{\sqrt{5}}{5}$=2.
点评 本题考查三角恒等变换与正余弦定理相结合,属于考试的重点,要求学生灵活掌握,属于中档题.

| A. | 1 | B. | $\sqrt{10}$ | C. | $\frac{{\sqrt{10}}}{2}$ | D. | 3 |
| A. | -$\frac{1}{2}$+$\frac{7}{2}$i | B. | -$\frac{1}{2}$-$\frac{7}{2}$i | C. | $\frac{1}{2}$-$\frac{7}{2}$i | D. | $\frac{1}{2}$+$\frac{7}{2}$i |
| A. | y=x2 | B. | y=2sinx | C. | y=2cosx | D. | y=2lnx |