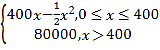Question

【题目】已知关于x的不等式组

(1) 若k＝1，求不等式组的解集；

(2) 若不等式组的整数解的集合为{－2}，求实数k的取值范围．

Answer 1

【答案】（1）{x|－＜x＜－1}；（2）－3≤k<2.

【解析】试题分析：（1）将k=1代入求解两个方程求交集即可.

（2）根据-2是方程的根，代入求得k的范围，再求出另一根，根据范围求解即可.

试题解析：

(1) 当k＝1时，由2x2＋7x＋5<0，得－＜x＜－1；

由x2－x－2>0，解得x<－1或x>2.

∴ 当k＝1时，不等式组的解集是{x|－＜x＜－1}．

(2) ∵ 不等式组的整数解的集合为{－2}，

∴ －2是2x2＋(2k＋5)x＋5k<0的解，

∴ k＜2，－k＞－.

又方程2x2＋(2k＋5)x＋5k＝0的两根为－k与－，

∴ 2x2＋(2k＋5)x＋5k<0的解是－<x<－k.

由于不等式组的整数解的集合为{－2}，

∴ －2<－k≤3，解得－3≤k<2，即k的取值范围是－3≤k<2.