题目内容
已知函数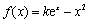 (其中
(其中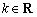 ,e是自然对数的底数).
,e是自然对数的底数).
(Ⅰ)若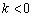 ,试判断函数
,试判断函数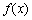 在区间
在区间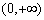 上的单调性;
上的单调性;
(Ⅱ)若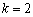 ,当
,当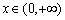 时,试比较
时,试比较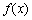 与2的大小;
与2的大小;
(Ⅲ)若函数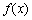 有两个极值点
有两个极值点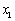 ,
,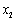 (
(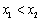 ),求k的取值范围,并证明
),求k的取值范围,并证明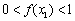 .
.
解析:(Ⅰ)由 可知,当
可知,当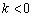 时,由于
时,由于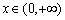 ,
, ,
,
故函数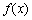 在区间
在区间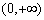 上是单调递减函数.
上是单调递减函数.
(Ⅱ)当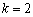 时,
时, ,则
,则 ,
,
令 ,
, ,
,
由于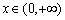 ,故
,故 ,于是
,于是 在
在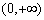 为增函数,
为增函数,
所以 ,即
,即 在
在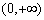 恒成立,
恒成立,
从而 在
在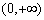 为增函数,故
为增函数,故 .
.
(Ⅲ)函数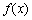 有两个极值点
有两个极值点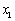 ,
,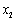 ,则
,则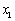 ,
,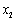 是
是 的两个根,
的两个根,
即方程 有两个根,设
有两个根,设 ,则
,则 ,
,
当 时,
时, ,函数
,函数 单调递增且
单调递增且 ;
;
当 时,
时, ,函数
,函数 单调递增且
单调递增且 ;
;
当 时,
时, ,函数
,函数 单调递减且
单调递减且 .
.
要使 有两个根,只需
有两个根,只需 .
.
故实数k的取值范围是 .
.
又由上可知函数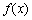 的两个极值点
的两个极值点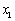 ,
,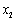 满足
满足 ,
,
由 ,得
,得 ,
,
∴ ,
,
由于 ,故
,故 ,
,
所以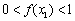 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, ,则不等式
,则不等式 的解集用区间表示为_________.
的解集用区间表示为_________.
 (B)
(B) (C)
(C) (D)
(D)
 .
. ,
, ,
, ,求△ABC的面积.
,求△ABC的面积.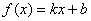 的图像经过点
的图像经过点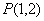 和
和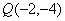 ,令
,令 ,记数列的前项和为
,记数列的前项和为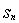 ,当
,当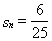 时,
时,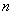 的值等于
的值等于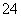 B.
B.  C.
C. 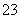 D.
D. 

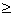 2,n
2,n N+), 则bn=
N+), 则bn=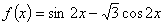 的图象( )
的图象( )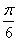 个单位 B.向左平移
个单位 B.向左平移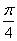 个单位 D.向左平移
个单位 D.向左平移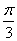 个单位
个单位