题目内容
4．作出下列函数的图象，并根据图象指出函数的值域．（1）y=$\frac{x|1-x|}{1{-x}^{2}}$；
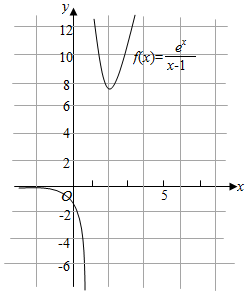
（2）y=$\frac{{e}^{x}}{x-1}$．
分析 （1）化简函数的解析式，然后画出函数的图象即可．
（2）利用函数的导数，判断函数的单调性以及函数的最值，然后画出函数的图象．
解答 -∞解：（1）y=$\frac{x|1-x|}{1{-x}^{2}}$=$\left\{\begin{array}{l}{\frac{x}{1+x}，x＞1}\\{-\frac{x}{1+x}，x＜1}\end{array}\right.$，
函数的图象如图：函数的值域为：（-∞，$\frac{1}{2}$）∪（1，+∞）．
（2）y=$\frac{{e}^{x}}{x-1}$．可得y′=$\frac{（x-2）{e}^{x}}{（x-1）^{2}}$，x∈（-∞，1）函数是减函数；
x∈（1，2），函数是减函数，y≥e2，x∈（2，+∞）时，函数是增函数．图象如图：
函数的值域为：（-∞，0）∪[e2，+∞）．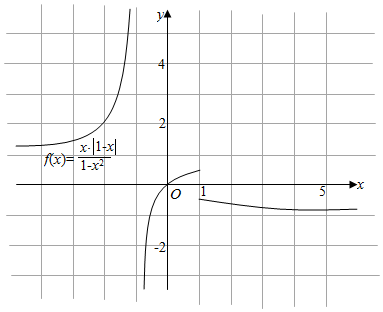
点评 本题考查函数的图象的画法，函数的单调性以及函数的值域的求法，考查数形结合以及计算能力．
练习册系列答案
相关题目
16．在△ABC中，A，B，C所对的边长分别为a，b，c，且$\frac{sinA}{cosB}=2sinC$，则△ABC的形状为（ ）
| A． | 等边三角形 | B． | 直角三角形 | C． | 等腰三角形 | D． | 等腰直角三角形 |
9．
在Rt△ABC中，∠C=$\frac{π}{2}$，AC=1，BC=$\sqrt{3}$，D是AB边上的动点，设BD=x，把△BDC沿DC翻折为△B′DC，若存在某个位置，使得异面直线B′C与AD所成的角为$\frac{π}{3}$，则实数x的取值范围是（ ）
在Rt△ABC中，∠C=$\frac{π}{2}$，AC=1，BC=$\sqrt{3}$，D是AB边上的动点，设BD=x，把△BDC沿DC翻折为△B′DC，若存在某个位置，使得异面直线B′C与AD所成的角为$\frac{π}{3}$，则实数x的取值范围是（ ）| A． | 0＜x＜$\frac{3-\sqrt{3}}{2}$ | B． | $\frac{3-\sqrt{3}}{2}$＜x＜2 | C． | 0＜x＜$\frac{2-\sqrt{3}}{2}$ | D． | $\frac{2-\sqrt{2}}{2}$＜x＜2 |
13．对于数列{xn}，若对任意n∈N*，都有xn+2-xn+1＜xn+1-xn成立，则称数列{xn}为“减差数列”．设${b_n}=2t-\frac{{t{n^2}-n}}{{{2^{n-1}}}}$，若数列${b_5}，{b_6}，{b_7}，…，{b_n}（{n≥5，n∈{N^*}}）$是“减差数列”，则实数t的取值范围是（ ）
| A． | $（{0，\frac{3}{5}}）$ | B． | $（{0，\frac{3}{5}}]$ | C． | $（{\frac{3}{5}，+∞}）$ | D． | $[{\frac{3}{5}，+∞}）$ |