题目内容
15．如图所示，四个正方体中，A，B为正方体的两个顶点，M，N，P分别为其所在棱的中点，能得到AB∥面MNP的图形的序号是（ ）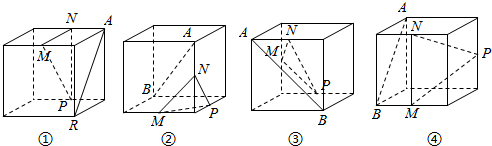
| A． | ①② | B． | ②④ | C． | ①③ | D． | ①④ |
分析 能得出AB∥面MNP，关键是看平面MNP中有没有与AB平行的直线，或者有没有过AB的平面与平面MNP平行．逐一判断即可．
解答 解：①∵面AB∥面MNP，
∴AB∥面MNP．
②若下底面中心为O，易知NO∥AB，NO?面MNP，
∴AB与面MNP不平行．
③易知AB∥MP，
∴AB∥面MNP．
④易知存在一直线MC∥AB，且MC?平面MNP，
∴AB与面MNP不平行．
故能得到AB∥面MNP的图形的序号是：①③．
故选：C．
点评 本题考查直线与平面平行的判定，考查了空间想象能力和推理论证能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
5．与双曲线3x2-y2=3的焦点相同且离心率互为倒数的椭圆方程为（ ）
| A． | x2+$\frac{{y}^{2}}{3}$=1 | B． | $\frac{{x}^{2}}{3}+{y}^{2}=1$ | C． | $\frac{{x}^{2}}{12}+\frac{{y}^{2}}{16}=1$ | D． | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$ |
6．椭圆x2+$\frac{{y}^{2}}{m}$=1的焦点在x轴上，长轴长是短轴长的两倍，则m的值为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 2 | D． | 4 |
3．已知a=30.2，b=0.2-3，c=（-3）0.2，则a，b，c的大小关系为（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞a＞b | D． | b＞c＞a |
20．f（x）=ax2+2（a-1）x+2在（-∞，4]上单调递减，则a的取值范围是（ ）
| A． | $a≤\frac{1}{5}$ | B． | $a≥\frac{1}{5}$ | C． | $0＜a≤\frac{1}{5}$ | D． | $0≤a≤\frac{1}{5}$ |
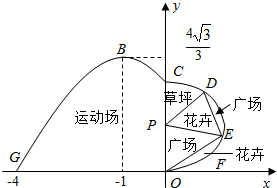如图，我市体育公园的运动休闲区域的平面图如图所示，在y轴左侧的运动区的边界曲线段是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），x∈[-4，0]时的图象且最高点B（-1，$\frac{4\sqrt{3}}{3}$），在y轴右侧的休闲区的边界曲线段是以P为圆心，CO为直径的半圆弧，D、E两点在半圆弧上，满足$\widehat{CE}$=$\widehat{DE}$．