题目内容
5.设$a>\frac{2}{3}$,且$x∈[-\frac{a}{2},-\frac{1}{3}]$时,|3x+1|-|2x+a|<-4x-2,求实数a的取值范围.分析 由题意可得a>-x+1对$x∈[-\frac{a}{2},-\frac{1}{3}]$恒成立,再根据利用函数的单调性求函数函数y的最大值为$\frac{a}{2}$+1,可得$\frac{1}{2}a+1<a$,由此解得a的范围.
解答 解:当$a>\frac{2}{3},且x∈[{-\frac{a}{2},-\frac{1}{3}}]$ 时,|3x+1|-|2x+a|=-5x-a-1,
不等式|3x+1|-|2x+a|<-4x-2化为-5x-a-1<-4x-2,
即a>-x+1对$x∈[-\frac{a}{2},-\frac{1}{3}]$恒成立.
∵函数y=-x+1是减函数,故函数y的最大值为$\frac{a}{2}$+1,
∴$\frac{1}{2}a+1<a$,解得a>2,又∵$a>\frac{2}{3}$,∴实数a的取值范围(2,+∞).
点评 本题主要考查绝对值不等式的解法,函数的恒成立问题,利用函数的单调性求函数的最值,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
15.如图所示,四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得到AB∥面MNP的图形的序号是( )
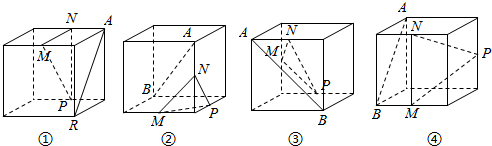

| A. | ①② | B. | ②④ | C. | ①③ | D. | ①④ |
10.设函数f(x)=x2-log2(2x+2).若0<b<1,则f(b)的值满足( )
| A. | f(b)>f(-$\frac{3}{4}$) | B. | f(b)>0 | C. | f(b)>f(2) | D. | f(b)<f(2) |
15.下列句子中,能确定一个集合的是( )
| A. | 难解的题目 | B. | 一年级全体学生 | ||
| C. | 所有很厚的书 | D. | 一年级所有高个子男生 |