题目内容
已知抛物线 与圆
与圆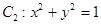
(I)求抛物线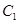 上一点
上一点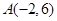 与圆
与圆 上一动点
上一动点 的距离的最小值;
的距离的最小值;
(II)将圆 向上平移
向上平移 个单位后能否使圆
个单位后能否使圆 在抛物线
在抛物线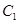 内并触及抛物线
内并触及抛物线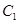 (与
(与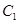 相切于顶点)的底部?若能,请求出
相切于顶点)的底部?若能,请求出 的值,若不能,试说明理由;
的值,若不能,试说明理由;
(III)设点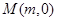 为
为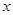 轴上一个动点,过
轴上一个动点,过 作抛物线
作抛物线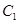 的两条切线,切点分别为
的两条切线,切点分别为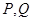 ,求证:直线
,求证:直线 过定点,并求出定点坐标。
过定点,并求出定点坐标。

【答案】
(1)所求最小值为 到圆心
到圆心 的距离减去圆的半径。即
的距离减去圆的半径。即
(2)假设平移后圆能触及抛物线 的底部,则
的底部,则 ,此时,圆方程为:
,此时,圆方程为: 与
与 联立,可解得
联立,可解得 或
或 与题设矛盾。故满足条件的
与题设矛盾。故满足条件的 的值不存在。
的值不存在。
(3)设 ,由
,由 得切线
得切线 的方程为
的方程为 ,又
,又 ,
,
且直线 过点
过点 ,故
,故 ,故
,故 在直线
在直线 上
上
同理点 在直线
在直线 上,故直线
上,故直线 方程为
方程为 ,
,
即直线 过定点
过定点
【解析】略

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.
已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点. 已知抛物线C:x2=2py(p>0)上一点A(m,4)到其焦点的距离为
已知抛物线C:x2=2py(p>0)上一点A(m,4)到其焦点的距离为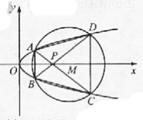 如图,已知抛物线
如图,已知抛物线