题目内容
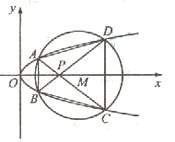
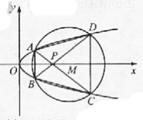 如图,已知抛物线
如图,已知抛物线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 、
、![]() 、
、![]() 四个点。
四个点。
(I)求![]() 得取值范围;
得取值范围;
(II)当四边形![]() 的面积最大时,求对角线
的面积最大时,求对角线![]() 、
、![]() 的交点
的交点![]() 坐标
坐标
分析:(I)这一问学生易下手。将抛物线![]() 与圆
与圆![]() 的方程联立,消去
的方程联立,消去![]() ,整理得
,整理得![]() .............(*)
.............(*)
抛物线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 、
、![]() 、
、![]() 四个点的充要条件是:方程(*)有两个不相等的正根即可.易得
四个点的充要条件是:方程(*)有两个不相等的正根即可.易得![]() .考生利用数形结合及函数和方程的思想来处理也可以.
.考生利用数形结合及函数和方程的思想来处理也可以.
(II)考纲中明确提出不考查求两个圆锥曲线的交点的坐标。因此利用设而不求、整体代入的 方法处理本小题是一个较好的切入点.
设四个交点的坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() 。
。
则由(I)根据韦达定理有![]() ,
,![]()
则![]()
![]()
令![]() ,则
,则![]() 下面求
下面求![]() 的最大值。
的最大值。
方法一:利用三次均值求解。三次均值目前在两纲中虽不要求,但在处理一些最值问题有时很方便。它的主要手段是配凑系数或常数,但要注意取等号的条件,这和二次均值类似。
![]()
![]()
当且仅当![]() ,即
,即![]() 时取最大值。经检验此时
时取最大值。经检验此时![]() 满足题意。
满足题意。
方法二:利用求导处理,这是命题人的意图。具体解法略。
下面来处理点![]() 的坐标。设点
的坐标。设点![]() 的坐标为:
的坐标为:![]() 以下略。
以下略。

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,已知抛物线
如图,已知抛物线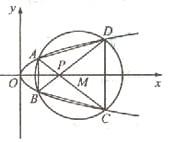 如图,已知抛物线
如图,已知抛物线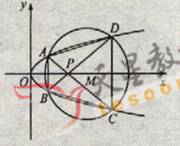 (22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线
(22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线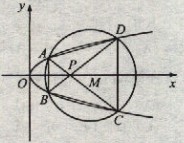
 如图,已知抛物线
如图,已知抛物线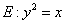
 与圆
与圆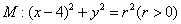 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。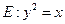
 与圆
与圆 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。