题目内容
若函数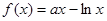 在
在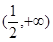 内单调递增,则
内单调递增,则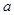 的取值范围为( )
的取值范围为( )
A.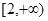 | B.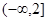 | C.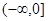 | D.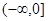 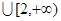 |
A
解析试题分析:因为 ,由函数
,由函数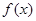 在
在 上单调递增,可知
上单调递增,可知 在
在 恒成立,即
恒成立,即 在
在 恒成立,而
恒成立,而 在
在 上单调递减,所以
上单调递减,所以 ,故选A.
,故选A.
考点:1.导数在单调性上的应用;2.不等式的恒成立问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
等比数列 中,
中, ,前3项和为
,前3项和为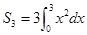 ,则公q的值是( )
,则公q的值是( )
| A. 1 | B.- | C. 1或- | D.- 1或- |
设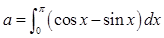 ,则二项式
,则二项式 展开式中的
展开式中的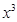 项的系数为( )
项的系数为( )
| A.20 | B.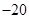 | C.160 | D. |
已知函数 ,求
,求 ( )
( )
A. | B.5 | C.4 | D.3 |
直线 的方向向量为
的方向向量为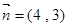 且过抛物线
且过抛物线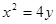 的焦点,则直线
的焦点,则直线 与抛物线围成的封闭图形面积为( )
与抛物线围成的封闭图形面积为( )
A.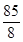 | B.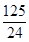 | C.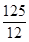 | D.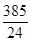 |
已知 为R上的可导函数,当
为R上的可导函数,当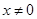 时,
时, ,则函数
,则函数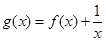 的零点分数为( )
的零点分数为( )
| A.1 | B.2 | C.0 | D.0或2 |
已知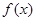 为R上的可导函数,且
为R上的可导函数,且 ,均有
,均有 ,则有 ( )
,则有 ( )
A. 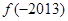 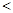 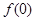 , ,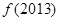 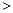  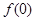 |
B. 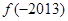 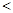 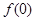 , ,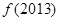 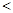  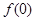 |
C. 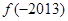 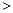 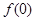 , ,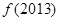 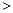  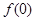 |
D. 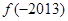 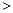 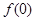 , ,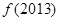 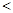  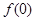 。 。 |
设函数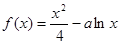 ,若
,若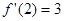 则
则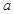 的值为( )
的值为( )
A.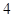 | B.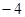 | C.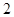 | D.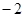 |
函数y=xex在点(1,e)处的切线方程为( ).
| A.y=ex | B.y=x-1+e |
| C.y=-2ex+3e | D.y=2ex-e |