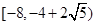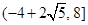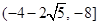题目内容
已知 为R上的可导函数,当
为R上的可导函数,当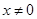 时,
时, ,则函数
,则函数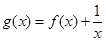 的零点分数为( )
的零点分数为( )
| A.1 | B.2 | C.0 | D.0或2 |
C
解析试题分析:因为函数 为R上的可导函数,当
为R上的可导函数,当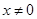 时,
时,  .即可
.即可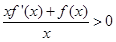 .令
.令 ,即
,即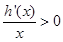 .所以可得
.所以可得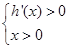 或
或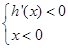 .所以当函数
.所以当函数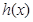 在
在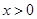 时单调递增,所以
时单调递增,所以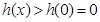 .即函数当
.即函数当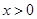 时,
时,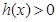 .同理
.同理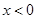 时,
时,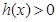 .又因为函数
.又因为函数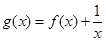 可化为
可化为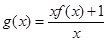 .所以当
.所以当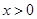 时,
时,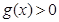 即与x轴没交点.当
即与x轴没交点.当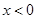 时,
时,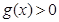 .所以函数
.所以函数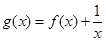 的零点个数为0.故选C.
的零点个数为0.故选C.
考点:1.函数的导数.2.函数的乘除的导数公式.3.函数的单调性.4.函数的最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图所示是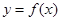 的导数
的导数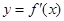 的图像,下列四个结论:
的图像,下列四个结论:
①  在区间
在区间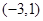 上是增函数;
上是增函数;
② 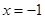 是
是 的极小值点;
的极小值点;
③  在区间
在区间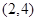 上是减函数,在区间
上是减函数,在区间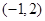 上是增函数;
上是增函数;
④ 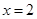 是
是 的极小值点.其中正确的结论是
的极小值点.其中正确的结论是
| A.①②③ |
| B.②③ |
| C.③④ |
| D.①③④ |
若函数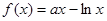 在
在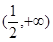 内单调递增,则
内单调递增,则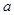 的取值范围为( )
的取值范围为( )
A.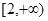 | B.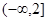 | C.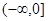 | D.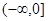 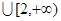 |
对于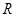 上可导的任意函数
上可导的任意函数 ,若满足
,若满足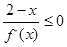 ,则必有( )
,则必有( )
A.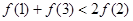 | B.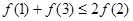 |
C.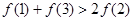 | D.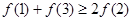 |
已知函数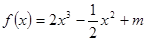 (m为常数)图象上A处的切线与
(m为常数)图象上A处的切线与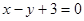 平行,则点A的横坐标是( )
平行,则点A的横坐标是( )
A. | B.1 | C.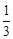 或 或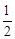 | D. 或 或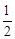 |
设曲线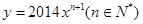 在点
在点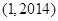 处的切线与
处的切线与 轴的交点的横坐标为
轴的交点的横坐标为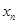 ,令
,令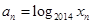 ,则
,则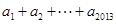 的值为( )
的值为( )
A.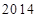 | B.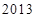 | C. | D.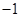 |
设函数f(x)=x3-4x+a(0<a<2)有三个零点x1,x2,x3,且x1<x2<x3,则下列结论正确的是( ).
| A.x1>-1 | B.x2<0 |
| C.x3>2 | D.0<x2<1 |
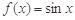 ,
,
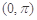 及直线x=a,
及直线x=a,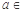
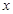 轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为
轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为 ,则
,则 的值是( )
的值是( )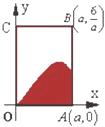
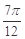
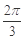
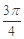
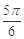
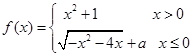 在点(1,2)处的切线与
在点(1,2)处的切线与 的图像有三个公共点,则
的图像有三个公共点,则 的取值范围是( )
的取值范围是( )