题目内容
等比数列 中,
中, ,前3项和为
,前3项和为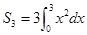 ,则公q的值是( )
,则公q的值是( )
| A. 1 | B.- | C. 1或- | D.- 1或- |
C
解析试题分析: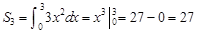 ,设公比为
,设公比为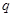 ,又
,又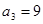 ,则
,则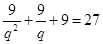 ,即
,即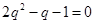 ,解得
,解得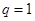 或
或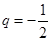 ,故选
,故选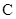 .
.
考点: 定积分 牛顿莱布尼茨公式

练习册系列答案
相关题目
若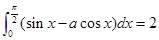 ,则实数
,则实数 等于( )
等于( )
A.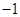 | B.1 | C.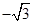 | D.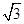 |
如图所示是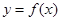 的导数
的导数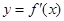 的图像,下列四个结论:
的图像,下列四个结论:
①  在区间
在区间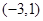 上是增函数;
上是增函数;
② 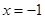 是
是 的极小值点;
的极小值点;
③  在区间
在区间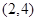 上是减函数,在区间
上是减函数,在区间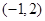 上是增函数;
上是增函数;
④ 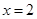 是
是 的极小值点.其中正确的结论是
的极小值点.其中正确的结论是
| A.①②③ |
| B.②③ |
| C.③④ |
| D.①③④ |
若函数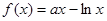 在
在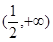 内单调递增,则
内单调递增,则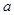 的取值范围为( )
的取值范围为( )
A.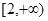 | B.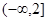 | C.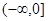 | D.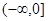 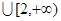 |
已知常数a,b,c都是实数,f(x)=ax3+bx2+cx-34的导函数为f′ (x),f′(x)≤0的解集为{x|-2≤x≤3},若f(x)的极小值等于-115,则a的值是( )
A.-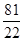 | B.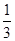 | C.2 | D.5 |
已知函数f(x)=ax-x3,对区间(0,1)上的任意x1,x2,且x1<x2,都有f(x2)-f(x1)>x2-x1成立,则实数a的取值范围为( )
| A.(0,1) | B.[4,+∞) | C.(0,4] | D.(1,4] |
函数f(x)=2lnx+x2-bx+a(b>0,a∈R)在点(b,f(b))处的切线斜率的最小值是( )
A.2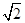 | B.2 | C.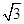 | D.1 |
已知函数f(x)=x3+ax2+x+2(a>0)的极大值点和极小值点都在区间(-1,1)内,则实数a的取值范围是( ).
| A.(0,2] | B.(0,2) | C.[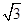 ,2) ,2) | D.(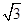 ,2) ,2) |