题目内容
某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(1)做出散点图;
(2)求线性回归方程
=bx+a;
(3)气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣的销售量.(
xiyi=1267,
=526)
| 月平均气温x(℃) | 17 | 13 | 8 | 2 |
| 月销售量y(件) | 24 | 33 | 40 | 55 |
(2)求线性回归方程
 |
| y |
(3)气象部门预测下个月的平均气温约为6℃,据此估计该商场下个月毛衣的销售量.(
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
| x | 2 i |
分析:(1)以月平均气温为x轴,月销售量y轴,根据表格数据,可得散点图;
(2)根据所给的数据,做出变量x,y的平均数,根据最小二乘法所需要的数据做出线性回归方程的系数b,在根据样本中心点一定在线性回归方程上,求出a的值,写出线性回归方程.
(2)根据上一问做出的线性回归方程和所给的下个月的平均气温,代入线性回归方程求出对应的y的值,这是一个预报值.
(2)根据所给的数据,做出变量x,y的平均数,根据最小二乘法所需要的数据做出线性回归方程的系数b,在根据样本中心点一定在线性回归方程上,求出a的值,写出线性回归方程.
(2)根据上一问做出的线性回归方程和所给的下个月的平均气温,代入线性回归方程求出对应的y的值,这是一个预报值.
解答: 解:(1)散点图如图.
解:(1)散点图如图.
(2)
=(17+13+8+2)÷4=10,…(3分)
b=
=
≈-2…(5分),
a=
-b
≈38-(-2)×10=58…(7分)
∴线性回归方程为
=-2x+58…(8分)
(3)气象部门预测下个月的平均气温约为6℃,据此估计,
该商场下个月毛衣的销售量为
≈-2.0×6+58.1≈46(件),
因此估计下月毛衣销量约为46件.…(10分)
 解:(1)散点图如图.
解:(1)散点图如图.(2)
. |
| x |
b=
| 1380-4×10×38 |
| 526-4×102 |
| 1267-4×10×38 |
| 526-4×102 |
a=
. |
| y |
. |
| x |
∴线性回归方程为
 |
| y |
(3)气象部门预测下个月的平均气温约为6℃,据此估计,
该商场下个月毛衣的销售量为
 |
| y |
因此估计下月毛衣销量约为46件.…(10分)
点评:本题考查线性回归方程,考查最小二乘法的应用,考查利用线性回归方程预报变量的值,是一个新课标中出现的新知识点,本题解题的关键是正确运算出线性回归方程系数b的值,本题是一个中档题目.

练习册系列答案
相关题目
某服装商场为了了解毛衣的月销售量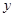 (件)与月平均气温
(件)与月平均气温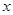 (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
|
月平均气温 |
17 |
13 |
8 |
2 |
|
月销售量 |
24 |
33 |
40 |
55 |
(1)做出散点图;
(2) 求线性回归方程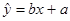 ;
;
(3)气象部门预测下个月的平均气温约为6ºC,据此估计该商场下个月毛衣的销售量.( 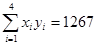 ,
,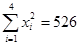 )
)
某服装商场为了了解毛衣的月销售量 (件)与月平均气温
(件)与月平均气温 (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
|
月平均气温 |
17 |
13 |
8 |
2 |
|
月销售量 |
24 |
33 |
40 |
55 |
由表中数据算出线性回归方程 中的
中的 ,气象部门预测下个月的平均气温约为6℃,据此估计,该商场下月毛衣的销售量约为
件。
,气象部门预测下个月的平均气温约为6℃,据此估计,该商场下月毛衣的销售量约为
件。
、某服装商场为了了解毛衣的月销售量y (件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
|
月平均气温x(℃) |
17 |
13 |
8 |
2 |
|
月销售量y(件) |
24 |
33 |
40 |
55 |
由表中数据算出线性回归方程 中的
中的 ,气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量约为________件.
,气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量约为________件.
