题目内容

数列{an}满足·a1+·a2+…+·an=5+2n(n∈N*),求数列{an}的通项公式及前n项和Sn的公式.

   

思路分析：在{an}满足的关系式中，设bn=·an,则左式即为{bn}的前n项和，由此可以利用{bn}的前n项和减去前n-1项和，先求bn，然后再求an.

    解:因为·a1+·a2+…+·an=2n+5,      ①

    所以当n≥2时，有

·a1+·a2+…+·an-1=2(n-1)+5.          ②

①式-②式可得·an=2(n≥2),

    所以an=2×2n=2n+1(n≥2).

    在①式中令n=1，可得·a1=2+5=7,

    即a1=14.所以an=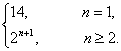

    显然S1=a1=14.

    当n≥2时，Sn=a1+a2+…+an

=14+23+24+…+2n+1

=14+=2n+2+6.

    综上可得Sn=2n+2+6(n∈N*).

练习册系列答案
相关题目
数列{an}满足a 1=
3
2
，a n+1=
a
2
n
-an+1（n∈N*），则m=
1
a1
+
1
a2
+
1
a3
+…+
1
a2012
的整数部分是（　　）
已知正项数列{an}满足
a
 
1
=P(0＜P＜1)，且
a
 
n+1
=
a
 
n
a
 
n
+1
，
（1）求数列的通项an；
（2）求证：
a
 
1
2
+
a
 
2
3
+
a
 
3
4
+…+
a
 
n
n+1
＜1．
（2012•三明模拟）若数列{an}满足a≤an≤b，其中a、b是常数，则称数列{an}为有界数列，a是数列{an}的下界，b是数列{an}的上界．现要在区间[-1，2）中取出20个数构成有界数列{bn}，并使数列{bn}有且仅有两项差的绝对值小于
1
m
，那么正数m的最小取值是（　　）
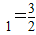数列{an}满足a，a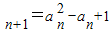（n∈N*），则m=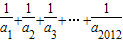的整数部分是（ ）
A．3
B．2
C．1
D．0
若数列{an}满足a≤an≤b，其中a、b是常数，则称数列{an}为有界数列，a是数列{an}的下界，b是数列{an}的上界．现要在区间[-1，2）中取出20个数构成有界数列{bn}，并使数列{bn}有且仅有两项差的绝对值小于，那么正数m的最小取值是（ ）
A．5
B．
C．7
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网