题目内容
数列{an}满足a 1=
,a n+1=
-an+1(n∈N*),则m=
+
+
+…+
的整数部分是( )
| 3 |
| 2 |
| a | 2 n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2012 |
分析:由a n+1=
-an+1,得
=
=
-
,即
=
-
,从而可求得
+
+
+…+
,通过作差可判断an+1≥an≥a1>1,又a2=
,a3=
>2,得a2013≥a3>2,
由此即可得到m的范围,从而可得答案.
| a | 2 n |
| 1 |
| an+1-1 |
| 1 |
| an(an-1) |
| 1 |
| an-1 |
| 1 |
| an |
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| an+1-1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 7 |
| 4 |
| 37 |
| 16 |
由此即可得到m的范围,从而可得答案.
解答:解:∵a n+1=
-an+1,
∴
=
=
-
,则
=
-
,
∴
+
+
+…+
=(
-
)+(
-
)+(
-
)+…+(
-
)
=
-
=2-
,
又an+1-an=an2-2an+1=(an-1)2≥0,
所以an+1≥an≥a1>1,
又a2=
,a3=
>2,则a2013≥a3>2,
所以m=2-
∈(1,2),故m的整数部分为1,
故选C.
| a | 2 n |
∴
| 1 |
| an+1-1 |
| 1 |
| an(an-1) |
| 1 |
| an-1 |
| 1 |
| an |
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| an+1-1 |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 1 |
| a1-1 |
| 1 |
| a2-1 |
| 1 |
| a2-1 |
| 1 |
| a3-1 |
| 1 |
| a3-1 |
| 1 |
| a4-1 |
| 1 |
| an-1 |
| 1 |
| an+1-1 |
=
| 1 |
| a1-1 |
| 1 |
| an+1-1 |
| 1 |
| an+1-1 |
又an+1-an=an2-2an+1=(an-1)2≥0,
所以an+1≥an≥a1>1,
又a2=
| 7 |
| 4 |
| 37 |
| 16 |
所以m=2-
| 1 |
| a2013-1 |
故选C.
点评:本题考查由数列递推式求数列的和,考查学生分析问题解决问题的能力,对能力要求较高.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
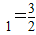 ,a
,a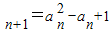 (n∈N*),则m=
(n∈N*),则m=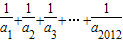 的整数部分是( )
的整数部分是( ) ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )
