题目内容
19．在面积为S的△ABC内部任取一点P，则△PBC的面积大于$\frac{S}{4}$的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{9}$ | D． | $\frac{9}{16}$ |
分析 在三角形ABC内部取一点P，要满足得到的三角形PBC的面积是原三角形面积的$\frac{1}{4}$，P点应位于图中DE的下方，然后用阴影部分的面积除以原三角形的面积即可得到答案
解答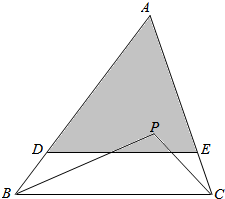 
解：记事件A={△PBC的面积超过$\frac{S}{4}$}，基本事件是三角形ABC的面积，（如图）
事件A的几何度量为图中阴影部分的面积（DE∥BC并且AD：AB=3：4），
因为阴影部分的面积是整个三角形面积的（$\frac{3}{4}$）2=$\frac{9}{16}$，
所以P（A）=$\frac{阴影部分}{三角形面积}=\frac{9}{16}$．
故选：D．
点评 本题考查了几何概型，解答此题的关键在于明确测度比是面积比，是基础的计算题．
练习册系列答案
相关题目
9．圆心在抛物线x2=2y上，并且和抛物线的准线及y轴都相切的圆的标准方程是（ ）
| A． | （x±2）2+（y-1）2=4 | B． | （x±1）2+（y-$\frac{1}{2}$）2=1 | C． | （x-1）2+（y±2）2=4 | D． | （x-$\frac{1}{2}$）2+（y±1）2=1 |
14．设全集为R，集合A={x∈R|x2＜4}，B={x|-1＜x≤4}，则A∩（∁RB）=（ ）
| A． | （-1，2） | B． | （-2，-1） | C． | （-2，-1] | D． | （-2，2） |
4．已知p：|x|＜2；q：x2-x-2＜0，则p是q的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
11．已知平面向量$\overrightarrow a$，$\overrightarrow b$满足|$\overrightarrow a$|=|$\overrightarrow b$|=1，（$\overrightarrow a$+2$\overrightarrow b$）（$\overrightarrow a$-$\overrightarrow b$）=-$\frac{1}{2}$，则与$\overrightarrow a$与$\overrightarrow b$的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
8．若△ABC中，cosA=$\frac{5}{13}$，cosB=$\frac{4}{5}$，则cosC的值为（ ）
| A． | $\frac{56}{65}$ | B． | -$\frac{56}{65}$ | C． | -$\frac{16}{65}$ | D． | $\frac{16}{65}$ |
9．已知实数x，y满足$\left\{{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}}\right.$，则目标函数z=2x-y的取值范围为（ ）
| A． | $[-1，\frac{1}{2}]$ | B． | $[\frac{1}{2}，5]$ | C． | [-1，5] | D． | [-1，3] |