题目内容
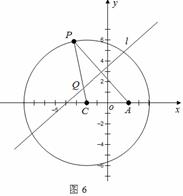
如图6,圆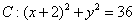 ,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.
,P是圆C上的任意一动点,A点坐标为(2,0),线段PA的垂直平分线l与半径CP交于点Q.
(1)求点Q的轨迹G的方程;
(2)已知B,D是轨迹G上不同的两个任意点,M为BD的中点. ①若M的坐标为M(2,1),求直线BD所在的直线方程;②若BD不经过原点,且不垂直于x轴,点O为轨迹G的中心. 求证:直线BD和直线OM的斜率之积是常数(定值).
解:(1)圆C的圆心为C(-2,0),半径r=6, .
.
连结 ,由已知得
,由已知得 ,
,
所以 .
.
根据椭圆的定义,点Q的轨迹G是中心在原点,以C、A为焦点,长轴长等于 的椭圆,
的椭圆,
即a=3,c=2, ,
,
所以,点Q的轨迹G的方程为 .
.
(2)①设B、D的坐标分别为 、
、 ,
,
则
两式相减,得 ,
,
当BD的中点M的坐标为(2,1)时,有 ,
,
所以 ,即
,即 .
.
故BD所在的直线方程为 ,即
,即 .
.
②证明:设 ,且
,且 ,
,
由①可知 ,
,
又
所以 (定值).
(定值).

练习册系列答案
相关题目
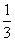 x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )
x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( ) 、
、 、
、 ,则三人中至少有一人达标的概率是 .
,则三人中至少有一人达标的概率是 . ,函数
,函数 ,
, ,则
,则 的值为
的值为 B.
B. C.
C. D.
D.
 (
( 为参数),C在点(0,3)处的切线为l,若以直角坐标原点为极点,以x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为 .
为参数),C在点(0,3)处的切线为l,若以直角坐标原点为极点,以x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为 .

 ,若函数
,若函数 有三个零点,则实数k的取值范围是
有三个零点,则实数k的取值范围是 B.
B.  C.
C.  D.
D. 
 的圆心
的圆心 ,且与直线
,且与直线 垂直的直线方程是( ) A.
垂直的直线方程是( ) A. B.
B. C.
C. D.
D. 
 和
和 ,则
,则 的值为 .
的值为 .