题目内容
某校从参加高三年级期中考试的学生600人中抽出60名学生，并统计了他们的物理成绩（成绩均为整数且满分为100分），把其中不低于50分的分成五段[50，60]，[60，70]，[70，80]，[80，90]，[90，100]后，由频率分布直方图直接知每段的频率分别为：0.15，0.15，0.3，0.25，0.05．则该校成绩低于50分的学生人数约为
60
60
．分析：先根据题意求出不低于50分的频率，然后利用各组的频率和为1求出低于50分的频率，最后乘以总人数求出该校成绩低于50分的学生人数．
解答：解：不低于50分的每段的频率分别为：0.15，0.15，0.3，0.25，0.05．
故不低于50分频率和为0.9，
因为各组的频率和等于1，故低于50的频率为：
f=1-0.9=0.1 （3分）
所以低于50（分）的人数为600×0.1=60（人） （5分）．
故答案为：60．
故不低于50分频率和为0.9，
因为各组的频率和等于1，故低于50的频率为：
f=1-0.9=0.1 （3分）
所以低于50（分）的人数为600×0.1=60（人） （5分）．
故答案为：60．
点评：用样本估计总体，是研究统计问题的一个基本思想方法．对于总体分布，总是用样本的频率分布对它进行估计，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某校从参加高三年级第一学期期末考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数，满分为100分），将数学成绩进行分组并根据各组人数制成如下频率分布表：
（Ⅰ）将上面的频率分布表补充完整，并估计本次考试全校85分以上学生的比例；
（Ⅱ）为了帮助成绩差的同学提高数学成绩，学校决定成立“二帮一”小组，即从成绩为[90，100]中任选出两位同学，共同帮助成绩在[40，50）中的某一个同学，试列出所有基本事件；若A1同学成绩为43分，B1同学成绩为95分，求A1、B1两同学恰好被安排在“二帮一”中同一小组的概率．
| 分 组 | 频 数 | 频 率 |
| [40，50 ） | 2 | 0.04 |
| [50，60 ） | 3 | 0.06 |
| [60，70 ） | 14 | 0.28 |
| [70，80 ） | 15 | 0.30 |
| [80，90 ） | ||
| [90，100] | 4 | 0.08 |
| 合 计 |
（Ⅱ）为了帮助成绩差的同学提高数学成绩，学校决定成立“二帮一”小组，即从成绩为[90，100]中任选出两位同学，共同帮助成绩在[40，50）中的某一个同学，试列出所有基本事件；若A1同学成绩为43分，B1同学成绩为95分，求A1、B1两同学恰好被安排在“二帮一”中同一小组的概率．
某校从参加高三年级期末考试的280名文科学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段[40，50），[50，60），…，[90，100]后得到如右部分频率分布直方图．观察图形的信息，回答下列问题：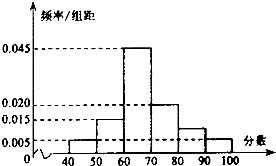
（2013•济宁一模）某校从参加高三年级期中考试的学生中随机统计了40名学生的政治成绩，这40名学生的成绩全部在40分至l00分之间，据此绘制了如图所示的样本频率分布直方图．
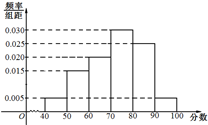某校从参加高三年级期末统考测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．