题目内容
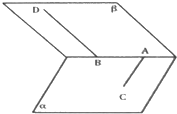 已知A、B是二面角α-a-β的棱a上两点,AB=4cm,在α内,AC⊥a,且AC=6cm,在β内BD⊥a且BD=8cm,当此二面角是60゜时,
已知A、B是二面角α-a-β的棱a上两点,AB=4cm,在α内,AC⊥a,且AC=6cm,在β内BD⊥a且BD=8cm,当此二面角是60゜时,(1)求CD的长;
(2)求B到面ACD的距离.
分析:(1)由AC⊥a,BD⊥a可得AB是异面直线AC、BD公垂线,故AC、BD所成角等于此二面角的平面角60゜,代入异面两点之间的距离公式,可得CD的长;
(2)作DE⊥平面a于E,连BE,利用等积法,求出四棱锥D-ABC的体积,进而可得B到面ACD的距离.
(2)作DE⊥平面a于E,连BE,利用等积法,求出四棱锥D-ABC的体积,进而可得B到面ACD的距离.
解答:解:(1)AB是异面直线AC、BD公垂线,AB=4cm,AC=6cm,BD=8cm
又AC、BD所成角等于此二面角的平面角60゜,
故CD=
=2
cm.
(2)在三棱锥D-ABC中,S△ABC=
AB?AC=12cm2.
作DE⊥平面a于E,连BE,
∵BD⊥a,则a⊥BE,故∠DBE=60゜,
∴DE=BD?sin60o=4
(cm),
于是VD-ABC=DE?S△ABC=16
.
又设B到平面ADC距离为d,连AD.
在△ACD中,AD2=80,CD2=68,AC2=36,
S△ACD=
=24.
故VB-ACD=
?d?24=16
,
∴d=2
cm.
又AC、BD所成角等于此二面角的平面角60゜,
故CD=
| AB2+AC2+BD2-2AC?BD?cos60° |
| 17 |
(2)在三棱锥D-ABC中,S△ABC=
| 1 |
| 2 |
作DE⊥平面a于E,连BE,
∵BD⊥a,则a⊥BE,故∠DBE=60゜,
∴DE=BD?sin60o=4
| 3 |
于是VD-ABC=DE?S△ABC=16
| 3 |
又设B到平面ADC距离为d,连AD.
在△ACD中,AD2=80,CD2=68,AC2=36,
S△ACD=
| 1 |
| 4 |
| 4?AD2?CD2-(AD2+CD2-AC2) |
故VB-ACD=
| 1 |
| 3 |
| 3 |
∴d=2
| 3 |
点评:本题考查的知识点是空间两点之间的距离及点到平面的距离,(1)的关键是熟练掌握异面直线上两点之间的距离公式,(2)的关键是利用等积法.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
已知A、B是球O表面上两点,AB=8.过AB作两个平面α、β,使球心O在平面α上,且O到平面β的距离为2
.如果二面角α-AB-β=60°,那么A、B两点的球面距离为( )
| 3 |
A、2
| ||
B、
| ||
C、
| ||
D、
|
己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
 .如果二面角α-AB-β=60°,那么A、B两点的球面距离为( )
.如果二面角α-AB-β=60°,那么A、B两点的球面距离为( ) π
π π
π

 .如果二面角α-AB-β=60°,那么A、B两点的球面距离为( )
.如果二面角α-AB-β=60°,那么A、B两点的球面距离为( ) π
π π
π
