题目内容
已知A、B是球O表面上两点,AB=8.过AB作两个平面α、β,使球心O在平面α上,且O到平面β的距离为2 .如果二面角α-AB-β=60°,那么A、B两点的球面距离为( )
.如果二面角α-AB-β=60°,那么A、B两点的球面距离为( )A.2
 π
πB.
 π
πC.

D.

【答案】分析:由已知中A、B是球O表面上两点,AB=8.过AB作两个平面α、β,使球心O在平面α上,作OO1⊥β,O1为垂足,取AB中点C,连接OC,O1C,易得∠O1CO是二面角α-AB-β的平面角,结合已知中,O到平面β的距离为2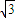 ,二面角α-AB-β=60°,我们易求出球的半径,易弦AB的球心角,代入弧长公式,即可求出答案.
,二面角α-AB-β=60°,我们易求出球的半径,易弦AB的球心角,代入弧长公式,即可求出答案.
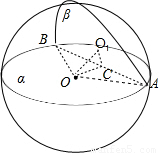
解答:解:作OO1⊥β,O1为垂足,取AB中点C,连接OC,O1C,
则OC⊥AB,O1C⊥AB,
∠O1CO是二面角α-AB-β的平面角,
所以∠O1CO=60°.
在Rt△OO1C中,
∵O到平面β的距离为2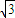 .
.
∴OO1=2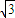 ,OC=4.
,OC=4.
连接OA、OB,由OC=AC=BC=4得∠AOB=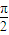 .
.
又球的半径OA=4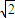 ,所以A、B两点间的球面距离为4
,所以A、B两点间的球面距离为4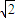 ×
×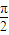 =2
=2 π
π
故选A
点评:本题考查球的截面及性质,球面距离,二面角等知识,考查学生的空间想象能力.求球面上两点间的球面距离时,必须先 找出这两点对球心所张的圆心角.
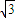 ,二面角α-AB-β=60°,我们易求出球的半径,易弦AB的球心角,代入弧长公式,即可求出答案.
,二面角α-AB-β=60°,我们易求出球的半径,易弦AB的球心角,代入弧长公式,即可求出答案.解答:解:作OO1⊥β,O1为垂足,取AB中点C,连接OC,O1C,
则OC⊥AB,O1C⊥AB,
∠O1CO是二面角α-AB-β的平面角,
所以∠O1CO=60°.
在Rt△OO1C中,
∵O到平面β的距离为2
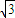 .
.
∴OO1=2
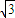 ,OC=4.
,OC=4.连接OA、OB,由OC=AC=BC=4得∠AOB=
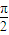 .
.又球的半径OA=4
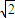 ,所以A、B两点间的球面距离为4
,所以A、B两点间的球面距离为4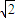 ×
×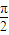 =2
=2 π
π故选A
点评:本题考查球的截面及性质,球面距离,二面角等知识,考查学生的空间想象能力.求球面上两点间的球面距离时,必须先 找出这两点对球心所张的圆心角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .如果二面角α-AB-β=60°,那么A、B两点的球面距离为( )
.如果二面角α-AB-β=60°,那么A、B两点的球面距离为( ) π
π π
π
