题目内容
设数列{bn}的前n项和为Sn,且bn=2-2Sn;数列{an}为等差数列,且a5=14,a7=20.(1)求数列{bn}的通项公式;
(2)若cn=an•bn(n=1,2,3…),Tn为数列{cn}的前n项和.求Tn.
【答案】分析:(1)由已知条件bn=2-2Sn;当n=1时先求出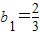 ,再利用bn-bn-1=-2(Sn-Sn-1)=-2bn
,再利用bn-bn-1=-2(Sn-Sn-1)=-2bn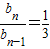 得到{bn}是以
得到{bn}是以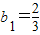 为首项,
为首项, 为公比的等比数列,利用等比数列的通项公式求出通项.
为公比的等比数列,利用等比数列的通项公式求出通项.
(2)求出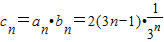 ,是一个等差数列与一个等比数列的乘积,所以利用错位相减的方法求出和.
,是一个等差数列与一个等比数列的乘积,所以利用错位相减的方法求出和.
解答:解:(1)由bn=2-2Sn,令n=1,则b1=2-2S1,又S1=b1
所以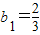 …(2分)
…(2分)
当n≥2时,由bn=2-2Sn,可得bn-bn-1=-2(Sn-Sn-1)=-2bn
即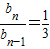 …(4分)
…(4分)
所以{bn}是以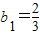 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,
于是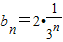 …(6分)
…(6分)
(2)数列{an}为等差数列,公差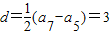 ,可得an=3n-1…(7分)
,可得an=3n-1…(7分)
从而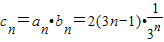
∴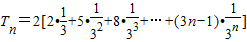 ,
,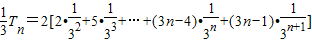 ∴
∴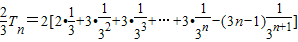 …(11分)
…(11分)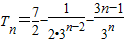 .…(12分)
.…(12分)
点评:求一个数列的前n项和,应该先求出数列的通项,根据通项的特点选择合适的求和方法.
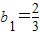 ,再利用bn-bn-1=-2(Sn-Sn-1)=-2bn
,再利用bn-bn-1=-2(Sn-Sn-1)=-2bn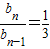 得到{bn}是以
得到{bn}是以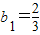 为首项,
为首项, 为公比的等比数列,利用等比数列的通项公式求出通项.
为公比的等比数列,利用等比数列的通项公式求出通项.(2)求出
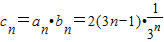 ,是一个等差数列与一个等比数列的乘积,所以利用错位相减的方法求出和.
,是一个等差数列与一个等比数列的乘积,所以利用错位相减的方法求出和.解答:解:(1)由bn=2-2Sn,令n=1,则b1=2-2S1,又S1=b1
所以
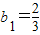 …(2分)
…(2分)当n≥2时,由bn=2-2Sn,可得bn-bn-1=-2(Sn-Sn-1)=-2bn
即
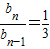 …(4分)
…(4分)所以{bn}是以
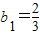 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,于是
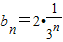 …(6分)
…(6分)(2)数列{an}为等差数列,公差
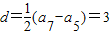 ,可得an=3n-1…(7分)
,可得an=3n-1…(7分)从而
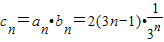
∴
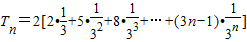 ,
,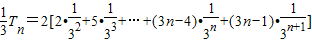 ∴
∴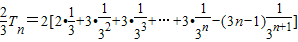 …(11分)
…(11分)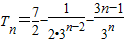 .…(12分)
.…(12分)点评:求一个数列的前n项和,应该先求出数列的通项,根据通项的特点选择合适的求和方法.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目