题目内容
9.求下列椭圆的长轴长、短轴长、焦距、离心率、焦点坐标与顶点坐标,并画出图形:(1)$\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{6}$=1;
(2)y2=5-5x2.
分析 直接利用椭圆的方程求解椭圆的几何量,求出所求结果即可.
解答 解:(1)$\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{6}$=1;可得a=$\sqrt{10}$,b=$\sqrt{6}$,c=2,
椭圆的长轴长:2$\sqrt{10}$、短轴长2$\sqrt{6}$,焦距4、离心率$\frac{\sqrt{10}}{5}$、焦点坐标(2,0),(-2,0)与顶点坐标($±\sqrt{10}$,0);(0,$±\sqrt{6}$).
椭圆的图形为:
(2)y2=5-5x2.化为:${x}^{2}+\frac{{y}^{2}}{5}=1$.可得a=$\sqrt{5}$,b=1,c=2,
椭圆的长轴长:2$\sqrt{5}$、短轴长2,焦距4、离心率$\frac{2\sqrt{5}}{5}$、焦点坐标(0,2),(0,-2)与顶点坐标(±2,0);(0,$±\sqrt{5}$).
椭圆的图形为:
点评 本题考查椭圆的简单性质的应用,基本知识的考查.

练习册系列答案
相关题目
19.集合A={x|lnx≥0},B={x|x2<9},则A∩B=( )
| A. | (1,3) | B. | [1,3) | C. | [1,+∞) | D. | [e,3) |
4.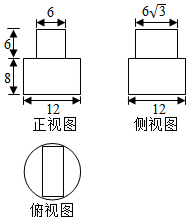 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | 360π+108$\sqrt{3}$ | B. | 288π+180$\sqrt{3}$ | C. | 288π+216$\sqrt{3}$ | D. | 360π+156$\sqrt{3}$ |
15.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$$•\overrightarrow{a}$=$\overrightarrow{a}$$•\overrightarrow{b}$=$\overrightarrow{b}$$•\overrightarrow{c}$=1,$\overrightarrow{a}$$•\overrightarrow{c}$=2,则|$\overrightarrow{a}$$+\overrightarrow{b}$$+\overrightarrow{c}$|的取值范围为( )
| A. | [0,+∞) | B. | [2$\sqrt{2}$,+∞) | C. | [2$\sqrt{3}$,+∞) | D. | [4,+∞) |
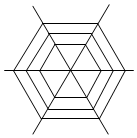 如图是一蜘蛛的辛勤劳动成果,已知该蜘蛛网从内到外由一系列嵌套的正六边形组成,其中最内部的正六边形的边长为a且从内至外正六边形的边长满足数量关系a,2a,3a,4a,…,其中最内部正六边形区域被称为“死亡区域”,只要猎物进入该区域则一定会被捕获,现在有一只蜜蜂飞向该蜘蛛网且其通过该蜘蛛网的最大范围不会超过从内至外的第三个正六边形,则猎物一定会被捕获的概率为$\frac{1}{9}$.
如图是一蜘蛛的辛勤劳动成果,已知该蜘蛛网从内到外由一系列嵌套的正六边形组成,其中最内部的正六边形的边长为a且从内至外正六边形的边长满足数量关系a,2a,3a,4a,…,其中最内部正六边形区域被称为“死亡区域”,只要猎物进入该区域则一定会被捕获,现在有一只蜜蜂飞向该蜘蛛网且其通过该蜘蛛网的最大范围不会超过从内至外的第三个正六边形,则猎物一定会被捕获的概率为$\frac{1}{9}$.