题目内容
14．
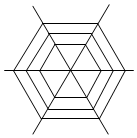如图是一蜘蛛的辛勤劳动成果，已知该蜘蛛网从内到外由一系列嵌套的正六边形组成，其中最内部的正六边形的边长为a且从内至外正六边形的边长满足数量关系a，2a，3a，4a，…，其中最内部正六边形区域被称为“死亡区域”，只要猎物进入该区域则一定会被捕获，现在有一只蜜蜂飞向该蜘蛛网且其通过该蜘蛛网的最大范围不会超过从内至外的第三个正六边形，则猎物一定会被捕获的概率为$\frac{1}{9}$．
分析 根据相似多边形的面积等于相似比平方，故最内部正六边形是从内至外的第三个正六边形面积的$\frac{1}{9}$，利用几何概型求概率
解答 解：根据相似多边形的面积等于相似比平方，故最内部正六边形是从内至外的第三个正六边形面积的$\frac{1}{9}$，
故猎物一定会被捕获的概率为$\frac{1}{9}$，
故答案为：$\frac{1}{9}$．
点评 本题考查了几何概型概率的求法，属于基础题．
练习册系列答案
相关题目
4．定义在[0，+∞）的函数f（x）的导函数为f′（x），对于任意的x≥0，恒有f′（x）＞f（x），a=e3f（2），b=e2f（3），则a，b的大小关系是（ ）
| A． | a＞b | B． | a＜b | C． | a=b | D． | 无法确定 |
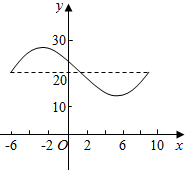函数y=Asin（ωx+θ）+b的图象如图所示，则此函数的解析式为y=y=10sin（$\frac{π}{8}$x+$\frac{3π}{4}$）+20．