题目内容

点A(3,2)为定点,点F是抛物线y2=2x的焦点,P点在抛物线y2=2x上移动,当|PA|+|PF|取得最小值时,求P点坐标.

思路分析:|PF|是焦半径(抛物线上任一点与焦点的连线段).把|PF|转化为点P到准线的距离.

解:(如图)l是抛物线的准线,过点P作准线l的垂线,垂足为H,则|PA|+|PF|=|PA|+|PH|.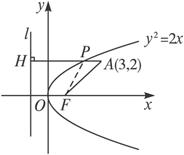

当H、P、A三点共线时,|PA|+|PF|有最小值,

∴点P的纵坐标为2.

∴x==2.

∴点P的坐标为(2,2).


练习册系列答案
相关题目
凸四边形PABQ中，其中A、B为定点，AB=
3
，P、Q为动点，满足AP=PQ=QB=1．
（1）写出cosA与cosQ的关系式；
（2）设△APB和△PQB的面积分别为S和T，求s2+T2的最大值，以及此时凸四边形PABQ的面积．
已知椭圆E的中心是坐标原点，焦点在坐标轴上，且椭圆过点A（-2，0），B（2，0），C（1，
32
）三点．
（1）求椭圆E的方程；
（2）若点D为椭圆E上不同于A，B的任意一点，F（-1，0），H（1，0），当△DFH内切圆的面积最大时，求内切圆圆心的坐标；
（3）若直线l：y=k（x+4），（k≠0）与椭圆E交于M，N两点，点M关于x轴的对称点为P，试问直线PN能否过定点F（-1，0），若是，请证明；若不是，请说明理由．
已知坐标平面上点M（x，y）与两个定点M1（26，1），M2（2，1）的距离之比等于5．
（1）求点M的轨迹方程，并说明轨迹是什么图形；
（2）记（1）中的轨迹为C，过点A（-2，3）的直线l被C所截得的线段的长为8，求直线l的方程．
（2008•普陀区二模）已知点E，F的坐标分别是（-2，0）、（2，0），直线EP，FP相交于点P，且它们的斜率之积为-
1
4
．
（1）求证：点P的轨迹在椭圆C：
x2
4
+y2=1上；
（2）设过原点O的直线AB交（1）题中的椭圆C于点A、B，定点M的坐标为(1，
1
2
)，试求△MAB面积的最大值，并求此时直线AB的斜率kAB；
（3）某同学由（2）题结论为特例作推广，得到如下猜想：
设点M（a，b）（ab≠0）为椭圆C：
x2
4
+y2=1内一点，过椭圆C中心的直线AB与椭圆分别交于A、B两点．则当且仅当kOM=-kAB时，△MAB的面积取得最大值．
问：此猜想是否正确？若正确，试证明之；若不正确，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网