题目内容
已知△ABC中角A，B，C所对边为a，b，c，且满足：2acosB=ccosB+bcosC，
(Ⅰ)求角B；
(Ⅱ)若b=5，S△ABC=2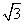
，求a+c的值。
(Ⅰ)求角B；
(Ⅱ)若b=5，S△ABC=2
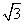，求a+c的值。解：(Ⅰ)由已知，得2sinAcosB=sinCcosB+sinBcosC，
即：2sinAcosB=sin(B+C)=sinA，
∴
。
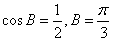(Ⅱ)由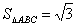
，得
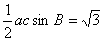，ac=4，
由余弦定理得25=a2+c2-ac，(a+c)2=25+12=37，
。
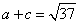即：2sinAcosB=sin(B+C)=sinA，
∴
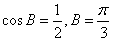。(Ⅱ)由
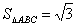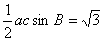，得，ac=4，由余弦定理得25=a2+c2-ac，(a+c)2=25+12=37，
。
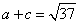练习册系列答案
相关题目
=（a，b）,
=（sinB,sinA）,
=（b-2,a-2）
，求△ABC的面积
=（a，b）,
=（sinB,sinA）,
=（b-2,a-2）（1）若
，求△ABC的面积
·(
+
)=
·
;②
·
=
;
·
=csinB;④
·(
-
)=b2-c2-2bccosA.其中正确的是_______________.(写出所有你认为正确的结论的序号)