题目内容
已知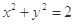 ,且
,且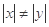 ,求
,求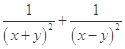 的最小值.
的最小值.
1.
解析试题分析:观察已知条件与所求式子,考虑到柯西不等式,可先将条件 化为
化为 ,此时,由柯西不等式得
,此时,由柯西不等式得 ,即
,即 ,当且仅当
,当且仅当 ,即
,即 ,或
,或 时,等号成立,从而可得
时,等号成立,从而可得 的最小值为1.
的最小值为1.
试题解析: ,
, ,
,  ,
,  , 当且仅当
, 当且仅当 ,或
,或 时
时 的最小值是1.
的最小值是1.
考点:柯西不等式.

练习册系列答案
相关题目
题目内容
已知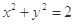 ,且
,且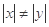 ,求
,求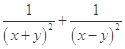 的最小值.
的最小值.
1.
解析试题分析:观察已知条件与所求式子,考虑到柯西不等式,可先将条件 化为
化为 ,此时,由柯西不等式得
,此时,由柯西不等式得 ,即
,即 ,当且仅当
,当且仅当 ,即
,即 ,或
,或 时,等号成立,从而可得
时,等号成立,从而可得 的最小值为1.
的最小值为1.
试题解析: ,
, ,
,  ,
,  , 当且仅当
, 当且仅当 ,或
,或 时
时 的最小值是1.
的最小值是1.
考点:柯西不等式.
