题目内容
已知函数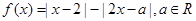 .
.
(1)当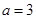 时,解不等式
时,解不等式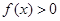 ;
;
(2)当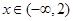 时,
时,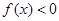 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)利用零点分段法,去分为 .三种情况绝对值,在每种情况下解不等式;求三次交集,最后再求一次并集,属于基础问题,关键是把绝对值去掉,并且不要忘记求交集;
.三种情况绝对值,在每种情况下解不等式;求三次交集,最后再求一次并集,属于基础问题,关键是把绝对值去掉,并且不要忘记求交集;
(2)当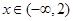 时,将其中一个绝对值去掉,问题转化为
时,将其中一个绝对值去掉,问题转化为 恒成立,
恒成立, ,利用公式将绝对值去掉,并且反解
,利用公式将绝对值去掉,并且反解 ,转化为
,转化为 或
或 恒成立的最值问题,因为.
恒成立的最值问题,因为.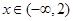 ,所以
,所以 只能大于等于
只能大于等于 的最大值.此题属于基础题型.
的最大值.此题属于基础题型.
试题解析:(1) 2分
2分
当 时,
时, ,即
,即 ,解得
,解得
当 时,
时, ,即
,即 ,解得
,解得
当 时,
时, ,即
,即 ,解得
,解得
不等式的解集为 5分
5分
(2) 恒成立
恒成立
即 10分
10分
考点:1解不等式;2.恒成立问题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
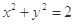 ,且
,且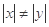 ,求
,求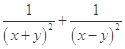 的最小值.
的最小值. ∈A,
∈A,
 A.
A.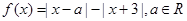 .
.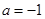 时,解不等式
时,解不等式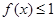 ;
; 时,
时,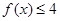 ,求a的取值范围.
,求a的取值范围. ,m∈R,且
,m∈R,且 的解集为
的解集为 .
. 的值;
的值; +,且
+,且 ,求
,求 的最小值.
的最小值. +
+ +
+ +
+ ≥
≥ .
.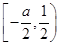 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围. ,求证:
,求证: .
.