题目内容
已知集合A={x|3≤x<7},B={x|2<x<10},C={x|5-a<x<a}.(1)求A∪B,(∁RA)∩B;
(2)若C⊆(A∪B),求a的取值范围.
【答案】分析:(1)把集合A和B用数轴表示出来,由图和运算定义求出并集、补集和交集;
(2)因集合C含有参数故需要考虑C=∅和C≠∅两种情况,再由子集的定义求出a的范围,最后要把结果并在一起.
解答:解:(1)由题意用数轴表示集合A和B如图:
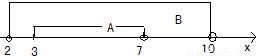
由图得,A∪B={x|2<x<10},∁RA={x|x<3或x≥7},
∴(∁RA)∩B={x|2<x<3或7≤x<10}(6分)
(2)由(1)知A∪B={x|2<x<10},
①当C=∅时,满足C⊆(A∪B),此时5-a≥a,得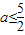 ;(8分)
;(8分)
②当C≠∅时,要C⊆(A∪B),则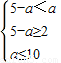 ,解得
,解得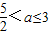 ;(12分)
;(12分)
由①②得,a≤3.
点评:本题考查了集合的混合运算和子集的定义应用,对于集合含有参数一定注意集合为空集时,故需要进行分类求解,当集合用不等式表示时,借助于数轴来求交集、并集和补集,更直观、准确,考查了数形结合和分类讨论思想.
(2)因集合C含有参数故需要考虑C=∅和C≠∅两种情况,再由子集的定义求出a的范围,最后要把结果并在一起.
解答:解:(1)由题意用数轴表示集合A和B如图:

由图得,A∪B={x|2<x<10},∁RA={x|x<3或x≥7},
∴(∁RA)∩B={x|2<x<3或7≤x<10}(6分)
(2)由(1)知A∪B={x|2<x<10},
①当C=∅时,满足C⊆(A∪B),此时5-a≥a,得
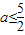 ;(8分)
;(8分)②当C≠∅时,要C⊆(A∪B),则
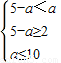 ,解得
,解得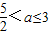 ;(12分)
;(12分)由①②得,a≤3.
点评:本题考查了集合的混合运算和子集的定义应用,对于集合含有参数一定注意集合为空集时,故需要进行分类求解,当集合用不等式表示时,借助于数轴来求交集、并集和补集,更直观、准确,考查了数形结合和分类讨论思想.

练习册系列答案
相关题目