题目内容
如图，△ABC是一个等边三角形遮阳棚，A、B为南北方向上两个定点，AB=2米，正东方向射出的太阳光与地面成40°角.为了使遮荫面△ABD的面积最大，遮阳棚△ABC与地面所成角的大小应为_______________；最大遮荫面积为______________平方米.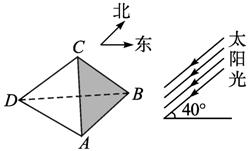
解析：设遮阳棚与地面所成的角为θ,取AB的中点E，连结CE、DE，在△CDE中，由正弦定理得
=
.
又CE=
,∴DE=
.
要使△ABD面积最大，只需使CE最大即可.
∴当140°-θ=90°，θ=50°时，(S△ABD)max=
.
答案：50° 
练习册系列答案
53随堂测系列答案
相关题目
（2013•普陀区二模）如图，△ABC是边长为1的正三角形，点P在△ABC所在的平面内，且
PA, 求二面角D-BC-A的大小；(结果用反三角函数值表示)
