题目内容
10. 我国古代名著《庄子•天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )
我国古代名著《庄子•天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )| ① | ② | ③ | |
| A | i≤7? | s=s-$\frac{1}{i}$ | i=i+1 |
| B | i≤128? | s=s-$\frac{1}{i}$ | i=2i |
| C | i≤7? | s=s-$\frac{1}{2i}$ | i=i+1 |
| D | i≤128? | s=s-$\frac{1}{2i}$ | i=2i |
| A. | A | B. | B | C. | C | D. | D |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知该程序的作用是累加并输出S的值,由此得出结论.
解答 解:程序运行过程中,各变量值如下表所示:
第1次循环:S=1,i=2,
第2次循环:S=1-$\frac{1}{2}$,i=4,
第3次循环:S=1-$\frac{1}{2}$-$\frac{1}{4}$-,i=16,…
依此类推,第6次循环:S=1-$\frac{1}{2}-\frac{1}{4}-\frac{1}{8}$…$-\frac{1}{64}$,i=64,
第7次循环,S=1-$\frac{1}{2}-\frac{1}{4}-…-\frac{1}{128}$,i=128,此时不满足条件,退出循环,
其中判断框内应填入的条件是:①i≤128?,②S=S-$\frac{1}{i}$,③i=2i;
故选:B.
点评 本题考查了程序框图的应用问题,其中程序填空是重要的考试题型,准确理解流程图的含义是解题的关键

练习册系列答案
相关题目
20. 如右图是正态分布$N(μ,{σ_1}^2),N(μ,{σ_2}^2),N(μ,{σ_3}^2)({σ_1},{σ_2},{σ_3}>0)$相应的曲线,那么σ1,σ2,σ3的大小关系是( )
如右图是正态分布$N(μ,{σ_1}^2),N(μ,{σ_2}^2),N(μ,{σ_3}^2)({σ_1},{σ_2},{σ_3}>0)$相应的曲线,那么σ1,σ2,σ3的大小关系是( )
 如右图是正态分布$N(μ,{σ_1}^2),N(μ,{σ_2}^2),N(μ,{σ_3}^2)({σ_1},{σ_2},{σ_3}>0)$相应的曲线,那么σ1,σ2,σ3的大小关系是( )
如右图是正态分布$N(μ,{σ_1}^2),N(μ,{σ_2}^2),N(μ,{σ_3}^2)({σ_1},{σ_2},{σ_3}>0)$相应的曲线,那么σ1,σ2,σ3的大小关系是( )| A. | σ1>σ2>σ3 | B. | σ3>σ2>σ1 | C. | σ1>σ3>σ2 | D. | σ2>σ1>σ3 |
1.sin43°cos17°+cos43°sin17°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
18.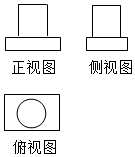 如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
 如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )| A. | 两个长方体 | B. | 两个圆柱 | ||
| C. | 一个长方体和一个圆柱 | D. | 一个球和一个长方体 |
15. 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )| A. | $\frac{π}{2}+1$ | B. | $\frac{π}{2}+3$ | C. | $\frac{3π}{2}+1$ | D. | $\frac{3π}{2}+3$ |
4.已知 f (x)=sin(x+$\frac{π}{2}$),g(x)=sin(π-x),则下列结论中正确的是( )
| A. | 函数 y=f (x)•g ( x) 的周期为 2 | |
| B. | 函数 y=f (x)•g ( x) 的最大值为 1 | |
| C. | 将f (x)的图象向左平移$\frac{π}{2}$个单位后得到 g(x)的图象 | |
| D. | y=f(x)+g(x)的一个对称中心是($\frac{3}{4}π$,0) |
5.三棱锥P-ABC的四个顶点都在球O的表面上,PA⊥平面ABC,AB⊥BC,PA=2,AB=BC=1,则球O的表面积为( )
| A. | $\sqrt{6}$π | B. | 6π | C. | 24π | D. | 2$\sqrt{6}$π |