题目内容
8. 如图所示,an=($\frac{1}{3}$)n,把数列{an}的各项排成如下三角形:记A(s,t)表示第s行第t个数,则A(6,2)=($\frac{1}{3}$)38.
如图所示,an=($\frac{1}{3}$)n,把数列{an}的各项排成如下三角形:记A(s,t)表示第s行第t个数,则A(6,2)=($\frac{1}{3}$)38.
分析 观察发现:数阵由连续的项的排列构成,且第m行有2m-1个数,根据等差数列求和公式,得出A(6,2)是数阵中第几个数字,即时数列{an}中的相序,再利用通项公式求出答案.
解答 解:由数阵可知,A(6,2)是数阵当中第1+3+5+7+9+11+2=38个数据,
也是数列{an}中的第38项,
而a38=($\frac{1}{3}$)38,
所以A(6,2)对应于数阵中的数是($\frac{1}{3}$)38.
故答案为:($\frac{1}{3}$)38
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
18.计算:$\frac{{\root{3}{a^2}•{{({a^{\frac{1}{6}}})}^4}}}{{\root{3}{a}}}$=( )
| A. | a | B. | a-2 | C. | $\root{3}{a^4}$ | D. | a4 |
17.已知复数z=(a-2)+ai(a∈R,i为虚数单位)为纯虚数,则$\int_{\;0}^{\;a}$($\sqrt{4-{x^2}}}$+x)dx的为( )
| A. | 2+π | B. | 2+$\frac{π}{2}$ | C. | 4+2π | D. | 4+4π |
18.若直线l1:ax+2y-8=0与l2:x+2y+4=0平行,则a的值为( )
| A. | -2 | B. | 1或2 | C. | 1 | D. | 1或-2 |
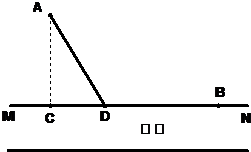 有一条笔直的河流,仓库A到河岸所在直线MN的距离是10km,AC⊥MN于C,码头B到C的距离为20km.现有一批货物要从A运到B.已知货物走陆路时,单位里程的运价是水路的2倍,货物走陆路到达D后再由水路到达B,问点D应选在离C多远处才能使总运费最低?
有一条笔直的河流,仓库A到河岸所在直线MN的距离是10km,AC⊥MN于C,码头B到C的距离为20km.现有一批货物要从A运到B.已知货物走陆路时,单位里程的运价是水路的2倍,货物走陆路到达D后再由水路到达B,问点D应选在离C多远处才能使总运费最低?