题目内容
已知直线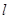 过点
过点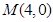 且与抛物线
且与抛物线 交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
交于A、B两点,以弦AB为直径的圆恒过坐标原点O.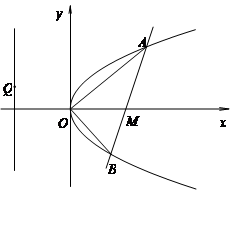
(1)求抛物线的标准方程;
(2)设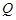 是直线
是直线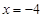 上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.
上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.
(1)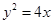 (2)详见解析.
(2)详见解析.
解析试题分析:(1)设直线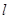 方程为
方程为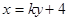 ,代入
,代入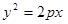 得
得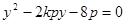
设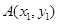 ,
,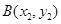 ,则有
,则有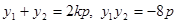 ,而
,而 ,
,
故
即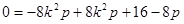 ,得
,得 ,所以抛物线方程为
,所以抛物线方程为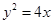 ;
;
(2)由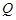 是直线
是直线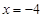 上任意一点,可设
上任意一点,可设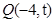 由(1)知
由(1)知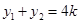 ,
,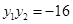 ,
,
∴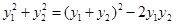 =
=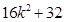 , ∵
, ∵ =
=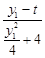 =
=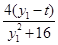 ,
,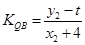 =
=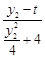 =
=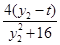 ,
,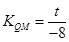
 +
+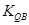 =
=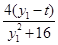 +
+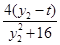 =
=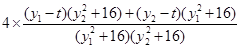
=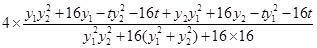 =
=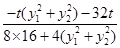 =
=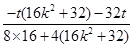 =
=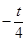 =
=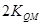 ,有等差中项的性质可知直线QA、QP、QB的斜率依次成等差数列.
,有等差中项的性质可知直线QA、QP、QB的斜率依次成等差数列.
试题解析:(1)设直线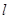 方程为
方程为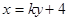 ,代入
,代入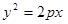 得
得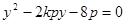
设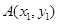 ,
,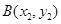 ,则有
,则有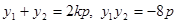 2分
2分
而 ,
,
故
即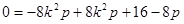 ,得
,得 ,所以抛物线方程为
,所以抛物线方程为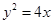 6分
6分
说明:取过M 点的特殊位置的直线求得抛物线的方程给满分.
(2)设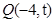 由(1)知
由(1)知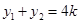 ,
,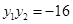 ,
,
∴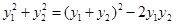 =
=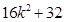 , ∵
, ∵ =
=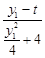 =
=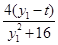 ,
,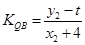 =
=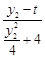 =
=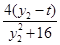 ,
,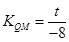 9分
9分 +
+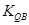 =
=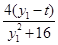 +
+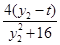 =
=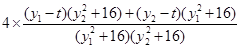
=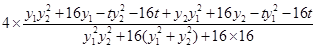
=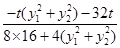 =
=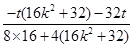 =
=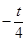 =
=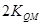

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
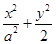 =1(a>
=1(a>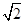 )的右焦点为F1,直线l:x=
)的右焦点为F1,直线l:x=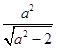 与x轴交于点A,若
与x轴交于点A,若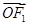 =2
=2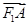 (其中O为坐标原点).
(其中O为坐标原点).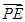 ·
·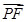 的最大值.
的最大值.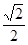 的椭圆
的椭圆 (
( )过点
)过点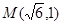
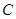 的方程;
的方程;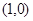 作斜率为
作斜率为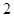 直线
直线 与椭圆相交于
与椭圆相交于 两点,求
两点,求 的长.
的长.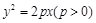 的焦点为双曲线
的焦点为双曲线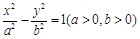 的一个焦点,且两条曲线都经过点
的一个焦点,且两条曲线都经过点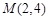 .
.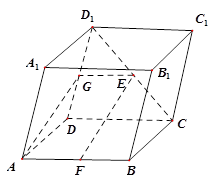
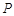 在抛物线上,且它与双曲线的左,右焦点构成的三角形的面积为4,求点
在抛物线上,且它与双曲线的左,右焦点构成的三角形的面积为4,求点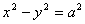 (其中
(其中 ).
).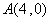 到双曲线上的点的最近距离为
到双曲线上的点的最近距离为 ,求
,求 的值;
的值;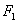 ,作倾斜角为
,作倾斜角为 的直线
的直线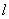 交双曲线于
交双曲线于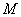 、
、 两点,其中
两点,其中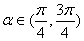 ,
,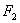 是双曲线的右焦点.求△
是双曲线的右焦点.求△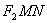 的面积
的面积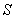 .
.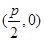 (p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.
(p为常数,p>0),B为x轴负半轴上的一个动点,动点M使得|AM|=|AB|,且线段BM的中点G在y轴上.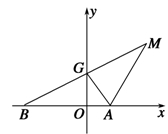
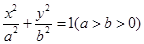 的右焦点为F2(1,0),点
的右焦点为F2(1,0),点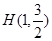 在椭圆上.
在椭圆上.
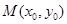 在圆
在圆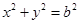 上,M在第一象限,过M作圆
上,M在第一象限,过M作圆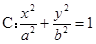
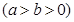 过点
过点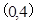 ,离心率为
,离心率为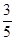 .
.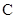 的方程;
的方程;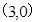 且斜率为
且斜率为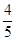 的直线被椭圆所截得线段的中点坐标.
的直线被椭圆所截得线段的中点坐标.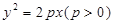 ,其准线方程为
,其准线方程为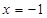 ,过准线与
,过准线与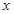 轴的交点
轴的交点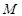 做直线
做直线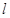 交抛物线于
交抛物线于 两点.
两点.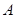 为
为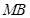 中点,求直线
中点,求直线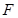 ,当
,当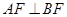 时,求
时,求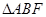 的面积.
的面积.