题目内容
12.已知正四棱锥P-ABCD的五个顶点都在同一个球面上,若该正四棱锥的底面边长为4,侧棱长为$2\sqrt{6}$,则此球的体积为36π.分析 利用勾股定理求出正四棱锥的高PM,再用射影定理求出球的半径,代入面积公式计算即可.
解答 解:如图所示,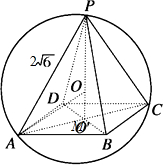
设球的半径为r,正方形的ABCD的对角线的交点为M,
则球心在直线PM上,
MC=$\frac{1}{2}$AC=2$\sqrt{2}$,
由勾股定理得PM=$\sqrt{{PC}^{2}{-MC}^{2}}$=$\sqrt{{(2\sqrt{6})}^{2}{-(2\sqrt{2})}^{2}}$=4,
再由射影定理得PC2=PM×2r,
即24=4×2r,
解得r=3,
所以此球的表面积为4πr2=36π.
故答案为:36π.
点评 本题考查了勾股定理、射影定理的应用以及球的表面积公式问题,是基础题目.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
3.某三棱锥的三视图如图所示,其体积V=( )
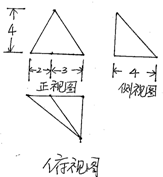

| A. | $\frac{80}{\begin{array}{l}3\end{array}}$ | B. | $\frac{40}{\begin{array}{l}3\end{array}}$ | C. | 80 | D. | 40 |
17.抛物线y2=4x的准线与x轴交于A点,焦点是F,P是位于x轴上方的抛物线上的任意一点,令m=$\frac{{|{PF}|}}{{|{PA}|}}$,当m取得最小值时,PA的斜率是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.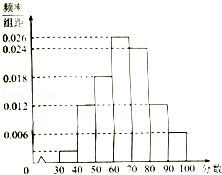 某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
(Ⅰ)估计该校高二年级学生在正式的数学学业水平考试中,成绩不合格的人数;
(Ⅱ)请你根据已知条件将下列2×2列联表补充完整,并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
 某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.(Ⅰ)估计该校高二年级学生在正式的数学学业水平考试中,成绩不合格的人数;
(Ⅱ)请你根据已知条件将下列2×2列联表补充完整,并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”?
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b=48 | 60 |
| 女生 | c=6 | d=34 | 40 |
| 合计 | 18 | 82 | n=100 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
1.不等式2x2-axy+3y2≥0对于任意x∈[1,2]及y∈[1,3]恒成立,则实数a的取值范围是( )
| A. | a≤2$\sqrt{2}$ | B. | a≤2$\sqrt{6}$ | C. | a≤5 | D. | a≤$\frac{9}{2}$ |
2.某工厂某产品产量y(千件)与单位成本x(元)满足线性回归方程$\widehat{y}$=75.7-2.13x,则以下说法中正确的是( )
| A. | 产量每增加1000件,单位成本下降2.13元 | |
| B. | 产量每减少1000件,单位成本下降2.13元 | |
| C. | 产量每增加1000件,单位成本上升2130元 | |
| D. | 产量每减少1000件,单位成本上升2130元 |



