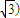题目内容
已知向量 ,
, ,其中A、B是△ABC的内角,
,其中A、B是△ABC的内角, .
.(1)求tanA•tanB的值;
(2)若a、b、c分别是角A、B、C的对边,当C最大时,求
 的值.
的值.
【答案】分析:(1)根据  推断出
推断出  =0,利用向量的数量积运算结合二倍角公式求得tanA•tanB;
=0,利用向量的数量积运算结合二倍角公式求得tanA•tanB;
(2)由于tanA•tanB= >0,利用基本不等式得出当且仅当
>0,利用基本不等式得出当且仅当  时,c取得最大值,再利用同角公式求出sinC,sinA,最后由正弦定理求
时,c取得最大值,再利用同角公式求出sinC,sinA,最后由正弦定理求 的值.
的值.
解答:解:(Ⅰ)由题意得 =0
=0
即 ,
,
-5cos(A+B)+4cos(A-B)=0
cosAcosB=9sinAsinB
∴tanA•tanB= .
.
(2)由于tanA•tanB= >0,且A、B是△ABC的内角,
>0,且A、B是△ABC的内角,
∴tanA>0,tanB>0
∴ =-
=-
当且仅当 取等号.
取等号.
∴c为最大边时,有 ,tanC=-
,tanC=- ,
,
∴sinC= ,sinA=
,sinA=
由正弦定理得: =
= .
.
点评:本题是中档题,考查三角函数的化简与求值,正弦定理的应用,基本不等式的知识,是一道综合题,考查学生分析问题解决问题的能力,公式的熟练程度决定学生的能力的高低.
 推断出
推断出  =0,利用向量的数量积运算结合二倍角公式求得tanA•tanB;
=0,利用向量的数量积运算结合二倍角公式求得tanA•tanB;(2)由于tanA•tanB=
 >0,利用基本不等式得出当且仅当
>0,利用基本不等式得出当且仅当  时,c取得最大值,再利用同角公式求出sinC,sinA,最后由正弦定理求
时,c取得最大值,再利用同角公式求出sinC,sinA,最后由正弦定理求 的值.
的值.解答:解:(Ⅰ)由题意得
 =0
=0即
 ,
,-5cos(A+B)+4cos(A-B)=0
cosAcosB=9sinAsinB
∴tanA•tanB=
 .
.(2)由于tanA•tanB=
 >0,且A、B是△ABC的内角,
>0,且A、B是△ABC的内角,∴tanA>0,tanB>0
∴
 =-
=-
当且仅当
 取等号.
取等号.∴c为最大边时,有
 ,tanC=-
,tanC=- ,
,∴sinC=
 ,sinA=
,sinA=
由正弦定理得:
 =
= .
.点评:本题是中档题,考查三角函数的化简与求值,正弦定理的应用,基本不等式的知识,是一道综合题,考查学生分析问题解决问题的能力,公式的熟练程度决定学生的能力的高低.

练习册系列答案
相关题目
 ,
, ,其中∠A,∠B为△ABC的内角,且
,其中∠A,∠B为△ABC的内角,且 .
. .
.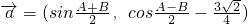 ,
,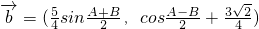 ,其中A、B是△ABC的内角,
,其中A、B是△ABC的内角, ⊥
⊥ ,
,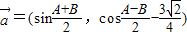 ,
,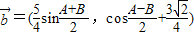 ,其中A、B是△ABC的内角,
,其中A、B是△ABC的内角,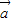 ⊥
⊥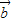 ,
,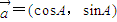 ,
,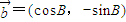 ,其中∠A,∠B为△ABC的内角,且
,其中∠A,∠B为△ABC的内角,且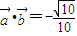 .
. .
.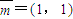 ,
,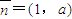 ,其中a为实数,当
,其中a为实数,当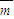 与
与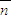 的夹角在区间
的夹角在区间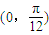 范围内变动时,实数a的取值范围是( )
范围内变动时,实数a的取值范围是( ) ,
,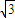 )
)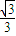 ,1)
,1)