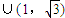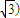题目内容
已知向量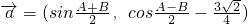 ,
,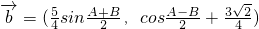 ,其中A、B是△ABC的内角,
,其中A、B是△ABC的内角, ⊥
⊥ ,
,
(Ⅰ)求tanAtanB的值;
(Ⅱ)求tanC的最大值.
解:(I)根据数量积的坐标运算公式,得
 •
• =
= sin2
sin2 +(cos2
+(cos2 -
- )=
)= [1-cos(A+B)]+
[1-cos(A+B)]+ [1+cos(A-B)]-
[1+cos(A-B)]-
= cos(A-B)-
cos(A-B)- cos(A+B)=
cos(A+B)= (cosAcosB+sinAsinB)-
(cosAcosB+sinAsinB)- (cosAcosB-sinAsinB)
(cosAcosB-sinAsinB)
= sinAsinB-
sinAsinB- cosAcosB
cosAcosB
∵ ⊥
⊥ ,
,
∴ •
• =0,即
=0,即 sinAsinB-
sinAsinB- cosAcosB=0,可得sinAsinB=
cosAcosB=0,可得sinAsinB= cosAcosB
cosAcosB
∴tanAtanB=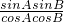 =
=
(II)∵A、B是△ABC的内角,
∴π-C=A+B,可得tanC=-tan(A+B)=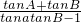 =-
=- (tanA+tanB)
(tanA+tanB)
∵A、B是三角形的内角,且tanAtanB= >0
>0
∴A、B都是锐角,tanA、tanB都是正数
因此tanA+tanB≥2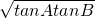 =
=
∴- (tanA+tanB)≤-
(tanA+tanB)≤- ×
× =-
=- ,即tanC≤-
,即tanC≤- ,
,
当且仅当tanA=tanB= 时,tanC的最大值为-
时,tanC的最大值为- .
.
分析:(I)根据数量积的坐标运算公式,将 •
• 展开,并用三角函数的降幂公式、和与差的余弦公式化简得:
展开,并用三角函数的降幂公式、和与差的余弦公式化简得: •
• =
= sinAsinB-
sinAsinB- cosAcosB,再由
cosAcosB,再由 ⊥
⊥ ,得到
,得到 sinAsinB-
sinAsinB- cosAcosB=0,最后可用同角三角函数的商数关系,得到tanAtanB=
cosAcosB=0,最后可用同角三角函数的商数关系,得到tanAtanB= ;
;
(II)根据三角形的内角和等于π,结合三角和的正切公式,可得tanC=-tan(A+B)=- (tanA+tanB),再经过讨论可得tanA、tanB都是正数,所以tanA+tanB≥2
(tanA+tanB),再经过讨论可得tanA、tanB都是正数,所以tanA+tanB≥2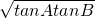 =
= ,从而得到当且仅当tanA=tanB=
,从而得到当且仅当tanA=tanB= 时,tanC的最大值为-
时,tanC的最大值为- .
.
点评:本题着重考查了三角函数的降幂公式、两角和的正切公式和基本不等式等知识点,属于中档题.
 •
• =
= sin2
sin2 +(cos2
+(cos2 -
- )=
)= [1-cos(A+B)]+
[1-cos(A+B)]+ [1+cos(A-B)]-
[1+cos(A-B)]-
=
 cos(A-B)-
cos(A-B)- cos(A+B)=
cos(A+B)= (cosAcosB+sinAsinB)-
(cosAcosB+sinAsinB)- (cosAcosB-sinAsinB)
(cosAcosB-sinAsinB)=
 sinAsinB-
sinAsinB- cosAcosB
cosAcosB∵
 ⊥
⊥ ,
,∴
 •
• =0,即
=0,即 sinAsinB-
sinAsinB- cosAcosB=0,可得sinAsinB=
cosAcosB=0,可得sinAsinB= cosAcosB
cosAcosB∴tanAtanB=
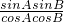 =
=
(II)∵A、B是△ABC的内角,
∴π-C=A+B,可得tanC=-tan(A+B)=
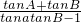 =-
=- (tanA+tanB)
(tanA+tanB) ∵A、B是三角形的内角,且tanAtanB=
 >0
>0∴A、B都是锐角,tanA、tanB都是正数
因此tanA+tanB≥2
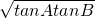 =
=
∴-
 (tanA+tanB)≤-
(tanA+tanB)≤- ×
× =-
=- ,即tanC≤-
,即tanC≤- ,
,当且仅当tanA=tanB=
 时,tanC的最大值为-
时,tanC的最大值为- .
.分析:(I)根据数量积的坐标运算公式,将
 •
• 展开,并用三角函数的降幂公式、和与差的余弦公式化简得:
展开,并用三角函数的降幂公式、和与差的余弦公式化简得: •
• =
= sinAsinB-
sinAsinB- cosAcosB,再由
cosAcosB,再由 ⊥
⊥ ,得到
,得到 sinAsinB-
sinAsinB- cosAcosB=0,最后可用同角三角函数的商数关系,得到tanAtanB=
cosAcosB=0,最后可用同角三角函数的商数关系,得到tanAtanB= ;
;(II)根据三角形的内角和等于π,结合三角和的正切公式,可得tanC=-tan(A+B)=-
 (tanA+tanB),再经过讨论可得tanA、tanB都是正数,所以tanA+tanB≥2
(tanA+tanB),再经过讨论可得tanA、tanB都是正数,所以tanA+tanB≥2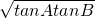 =
= ,从而得到当且仅当tanA=tanB=
,从而得到当且仅当tanA=tanB= 时,tanC的最大值为-
时,tanC的最大值为- .
.点评:本题着重考查了三角函数的降幂公式、两角和的正切公式和基本不等式等知识点,属于中档题.

练习册系列答案
相关题目
 ,
, ,其中∠A,∠B为△ABC的内角,且
,其中∠A,∠B为△ABC的内角,且 .
. .
.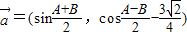 ,
,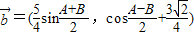 ,其中A、B是△ABC的内角,
,其中A、B是△ABC的内角,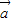 ⊥
⊥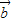 ,
,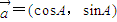 ,
,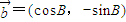 ,其中∠A,∠B为△ABC的内角,且
,其中∠A,∠B为△ABC的内角,且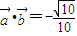 .
. .
.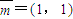 ,
,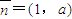 ,其中a为实数,当
,其中a为实数,当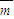 与
与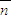 的夹角在区间
的夹角在区间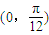 范围内变动时,实数a的取值范围是( )
范围内变动时,实数a的取值范围是( ) ,
,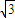 )
)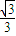 ,1)
,1)