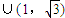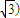题目内容
已知向量 ,
, ,其中∠A,∠B为△ABC的内角,且
,其中∠A,∠B为△ABC的内角,且 .
.
(Ⅰ)求tan(A+B)的值;
(Ⅱ)若 .
.
解:(Ⅰ)△ABC中,由 可得 cosAcosB-sinAsinB=cos(A+B)=-
可得 cosAcosB-sinAsinB=cos(A+B)=- ,
,
故sin(A+B)= ,故tan(A+B)=
,故tan(A+B)= =-3.
=-3.
(Ⅱ)∵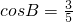 ,
,
∴sinB= ,
,
∴sinA=sin[(A+B)-B]=sin(A+B)cosB-cos(A+B)sinB= .
.
分析:(Ⅰ)△ABC中,由 可得cos(A+B)=-
可得cos(A+B)=- ,从而求出sin(A+B)=
,从而求出sin(A+B)= ,由此求得tan(A+B)的值.
,由此求得tan(A+B)的值.
(Ⅱ)由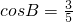 ,求得 sinB=
,求得 sinB= ,再根据sinA=sin[(A+B)-B],利用两角差的正弦公式求得结果.
,再根据sinA=sin[(A+B)-B],利用两角差的正弦公式求得结果.
点评:本题主要考查两个向量的数量积的定义,同角三角函数的基本关系,两角差的正弦公式的应用,属于中档题.
 可得 cosAcosB-sinAsinB=cos(A+B)=-
可得 cosAcosB-sinAsinB=cos(A+B)=- ,
,故sin(A+B)=
 ,故tan(A+B)=
,故tan(A+B)= =-3.
=-3.(Ⅱ)∵
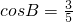 ,
,∴sinB=
 ,
,∴sinA=sin[(A+B)-B]=sin(A+B)cosB-cos(A+B)sinB=
 .
.分析:(Ⅰ)△ABC中,由
 可得cos(A+B)=-
可得cos(A+B)=- ,从而求出sin(A+B)=
,从而求出sin(A+B)= ,由此求得tan(A+B)的值.
,由此求得tan(A+B)的值.(Ⅱ)由
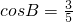 ,求得 sinB=
,求得 sinB= ,再根据sinA=sin[(A+B)-B],利用两角差的正弦公式求得结果.
,再根据sinA=sin[(A+B)-B],利用两角差的正弦公式求得结果.点评:本题主要考查两个向量的数量积的定义,同角三角函数的基本关系,两角差的正弦公式的应用,属于中档题.

练习册系列答案
相关题目
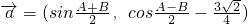 ,
,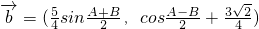 ,其中A、B是△ABC的内角,
,其中A、B是△ABC的内角, ⊥
⊥ ,
,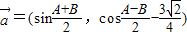 ,
,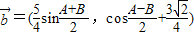 ,其中A、B是△ABC的内角,
,其中A、B是△ABC的内角,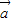 ⊥
⊥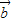 ,
,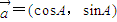 ,
,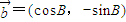 ,其中∠A,∠B为△ABC的内角,且
,其中∠A,∠B为△ABC的内角,且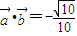 .
. .
.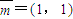 ,
,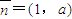 ,其中a为实数,当
,其中a为实数,当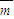 与
与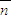 的夹角在区间
的夹角在区间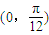 范围内变动时,实数a的取值范围是( )
范围内变动时,实数a的取值范围是( ) ,
,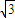 )
)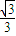 ,1)
,1)