题目内容
设数列{an}的前n项和为Sn,a1=2,对任意的n∈N*,向量
=(-1,an),
=(an+1,q)(q是常数,q>0)都满足
⊥
,求
.
| a |
| b |
| a |
| b |
| lim |
| n→∞ |
| Sn |
| Sn+1 |
∵
⊥
,∴
•
=-an+1+anq=0,即
=q,故数列{an}是以2为首项、以q为公比的等比数列.
当q=1时,
=
=1;
当q≠1时,
=
=
.
| a |
| b |
| a |
| b |
| an+1 |
| an |
当q=1时,
| lim |
| n→∞ |
| Sn |
| Sn+1 |
| lim |
| n→∞ |
| na1 |
| (n+1)a1 |
当q≠1时,
| lim |
| n→∞ |
| Sn |
| Sn+1 |
| lim |
| n→∞ |
| 1-qn |
| 1-qn+1 |
|

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 (1)若
(1)若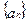 是等差数列,则
是等差数列,则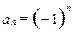 ,当
,当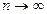 时,数列
时,数列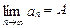 ,则
,则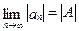 。
。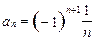 ,则
,则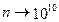 ,数列
,数列 满足
满足 ,则
,则 ____________.
____________.
 ,写出
,写出 的一个通项公式
的一个通项公式 =________
=________ {n[(1+
{n[(1+ )2
)2 ]}=
]}=