题目内容
18.已知三棱柱ABC-A1B1C1的侧棱与底面垂直,体积为$\frac{3\sqrt{3}}{2}$,底面是边长为$\sqrt{3}$的正三角形,则三棱柱ABC-A1B1C1的外接球体积为$\frac{8\sqrt{2}}{3}$π.分析 先根据题意画出图形,再设三棱柱外接球的球半径为r,利用在直角三角形ADO中的边的关系求出球半径,最后利用球的体积公式即可求出这个三棱柱的外接球的体积.
解答 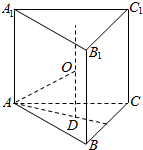 解:设三棱柱外接球的球心为O,球半径为r,
解:设三棱柱外接球的球心为O,球半径为r,
三棱柱的底面三角形ABC的中心为D,如图,
∵三棱柱ABC-A1B1C1的侧棱与底面垂直,体积为$\frac{3\sqrt{3}}{2}$,底面是边长为$\sqrt{3}$的正三角形,
∴$\frac{\sqrt{3}}{4}×3×A{A}_{1}$=$\frac{3\sqrt{3}}{2}$,
∴AA1=2,∴OD=1
又在正三角形ABC中,AB=$\sqrt{3}$,则AD=1,
∴在直角三角形ADO中,OA2=OD2+AD2有r2=12+12,
∴r=$\sqrt{2}$,
则这个三棱柱的外接球的体积为V=$\frac{4π}{3}$×r3=$\frac{8\sqrt{2}}{3}$π.
故答案为:$\frac{8\sqrt{2}}{3}$π.
点评 本题是基础题,考查几何体的外接球的体积的应用,三棱柱体积的求法,考查计算能力.

练习册系列答案
相关题目
9.为了了解全校1740名学生的身高情况,从中抽取140名学生进行测量,下列说法正确的是( )
| A. | 总体是1740 | B. | 个体是每一个学生 | ||
| C. | 样本是140名学生 | D. | 样本容量是140 |
6.已知函数f(x)=(a-2)x-ax3在区间[-1,1]上的最大值为2,则a的取值范围是( )
| A. | [2,10] | B. | [-1,8] | C. | [-2,2] | D. | [0,9] |
3.曲线C:y=xlnx在点M(e,e)处的切线方程为( )
| A. | y=x-e | B. | y=x+e | C. | y=2x-e | D. | y=2x+e |
10.函数f(x)=sin(2x+φ)(0<φ<π),若将函数y=f(x)的图象向左平移$\frac{π}{6}$个单位后所得图象对应的函数为偶函数,则实数φ的值为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |