题目内容
15．已知$f（x）=\frac{sinx}{1+cosx}$，x∈（-π，0）．当f'（x0）=2时，x0等于（ ）| A． | $\frac{2π}{3}$ | B． | $-\frac{2}{3}π$ | C． | $-\frac{π}{3}$ | D． | $-\frac{π}{6}$ |
分析 首先求得f'（x）=$\frac{1}{1+cosx}$，然后根据f'（x0）=2进行解答．
解答 解：由$f（x）=\frac{sinx}{1+cosx}$，得：
f'（x）=$\frac{（sinx）′（1+cosx）-sinx（1+cosx）′}{（1+cosx）^{2}}$
=$\frac{cosx+co{s}^{2}x+si{n}^{2}x}{（1+cosx）^{2}}$=$\frac{1+cosx}{（1+cosx）^{2}}$=$\frac{1}{1+cosx}$．
所以f'（x0）=$\frac{1}{1+cos{x}_{0}}$=2，
所以cosx0=-$\frac{1}{2}$，
因为x∈（-π，0）．
所以x=-$\frac{2}{3}$π．
故选B．
点评 本题主要考察了同角三角函数关系式，考查计算能力，属于基础题型．
练习册系列答案
口算能手系列答案
相关题目
10．下列各组函数中，表示同一函数的是（ ）
| A． | y=1，y=x0 | B． | $y=x\;，\;y=\root{3}{x^3}$ | ||
| C． | $y=\sqrt{x-1}•\sqrt{x+1}\;，\;y=\sqrt{{x^2}-1}$ | D． | $y=|x|\;，\;y={（\sqrt{x}）^2}$ |
4．已知函数f（x）=$\left\{\begin{array}{l}{（a-2）x，x≥2}\\{（\frac{1}{2}）^{x}-1，x＜2}\end{array}\right.$，满足对任意的实数x1≠x2，都有$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＜0成立，则实数a的取值范围为（ ）
| A． | （-∞，2） | B． | [$\frac{13}{4}$，2） | C． | [$\frac{13}{8}$，2） | D． | （-∞，$\frac{13}{8}$] |
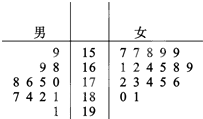某部队为了在大阅兵中树立军队的良好形象，决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员，这30名军人的身高如图：单位：cm