题目内容

在区间[0，2π]内使得sinx＞cosx的x的取值范围是

A.
$数学公式$
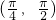
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

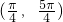
D
分析：sinx＞cosx? $\text{[math]}$ sin（x- $\text{[math]}$ ）＞0，x∈[0，2π]，利用正弦函数的性质即可求得答案．
解答：∵sinx＞cosx，
∴sinx-cosx＞0，
即 $\text{[math]}$ sin（x- $\text{[math]}$ ）＞0，
∴sin（x- $\text{[math]}$ ）＞0．
∵x∈[0，2π]，
∴- $\text{[math]}$ ≤x- $\text{[math]}$ ≤ $\text{[math]}$ ，
∵0＜x- $\text{[math]}$ ＜π，即 $\text{[math]}$ ＜x＜ $\text{[math]}$ 时，sin（x- $\text{[math]}$ ）＞0，
∴在区间[0，2π]内使得sinx＞cosx的x的取值范围是（ $\text{[math]}$ ， $\text{[math]}$ ）．
故选D．
点评：本题考查正弦函数的性质，考查辅助角公式的应用，考查转化思想，属于中档题．

练习册系列答案

Happy寒假作业快乐寒假系列答案

金象教育U计划学期系统复习寒假作业系列答案

八斗才火线计划寒假西安交通大学出版社系列答案

伴你成长橙色寒假系列答案

帮你学寒假作业系列答案

备战中考寒假系列答案

创新大课堂系列丛书寒假作业系列答案

创新自主学习寒假新天地系列答案

创优教学寒假作业年度总复习系列答案

导学练寒假作业云南教育出版社系列答案

相关题目

，sinx-cosx，2cos

依次成等比数列，则x在区间[0，2π）内的解集为

若查表求得f(0.96)=0.8315，f(1.81)=0.9648，f(0.5)=0.6915，f(2)=0.9772，则标准正态总体在区间(-1.81，0.96)内取值的概率为________；正态总体N(2，1²)在区间(0，2.5)内取值的概率为________。

已知 $数学公式$ 依次成等比数列，则x在区间[0，2π）内的解集为________．

，sinx-cosx，2cos

依次成等比数列，则x在区间[0，2π）内的解集为______．

依次成等比数列，则x在区间[0，2π）内的解集为．