题目内容
8．
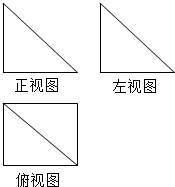一个几何体的三视图如图所示，其中主视图和左视图是腰长为2的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则该球的表面积是（ ）| A． | 32$\sqrt{3}$π | B． | 4$\sqrt{3}$π | C． | 48π | D． | 12π |
分析 作出几何体的直观图，根据棱锥的结构特征计算外接球的半径，得出球的面积．
解答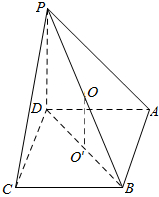 
解：由三视图可知几何体为底面为正方形的四棱锥P-ABCD，PD⊥平面ABCD，PD=AD=2，
取BD中点O'，PB中点O，连结OO'，则OO'∥PA，∴OO'⊥平面ABCD，
∴O为四棱锥P-ABCD的外接球球心，∵OO'=$\frac{1}{2}PD$=1，O'B=$\frac{1}{2}BD$=$\sqrt{2}$，∴OB=$\sqrt{OO{'}^{2}+O'{B}^{2}}$=$\sqrt{3}$．
∴棱锥外接球的面积S=4πOB2=12π．
故选D．
点评 本题考查了棱锥的三视图和结构特征，棱锥与球的关系，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
19．某几何体的三视图如图所示，则该几何体的体积为（ ）
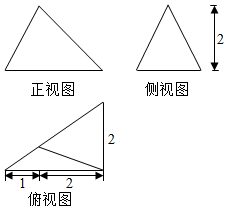
| A． | $\frac{4}{3}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | 3 | D． | 2 |
3．在等腰梯形ABCD中，AB∥CD，且|AB|=2，|AD|=1，|CD|=2x，其中x∈（0，1），以A，B为焦点且过点D的双曲线的离心率为e1，以C，D为焦点且过点A的椭圆的离心率为e2，若对任意x∈（0，1）都有不等式$t＜\frac{{{{（{e_1}+{e_2}）}^2}}}{8}$恒成立，则t的最大值为（ ）
| A． | $\frac{7}{4}$ | B． | $\frac{3}{8}$ | C． | $\frac{5}{8}$ | D． | $\frac{5}{4}$ |
13．若A点坐标为（1，1），F1是椭圆5x2+9y2=45的左焦点，点P是该椭圆上的动点，则|PA|+|PF1|的最大值为（ ）
| A． | $6-\sqrt{2}$ | B． | $6+\sqrt{2}$ | C． | $5+\sqrt{2}$ | D． | $7+\sqrt{2}$ |
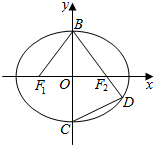如图，在平面直角坐标系xOy中，F1，F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，B，C分别为椭圆上、下顶点，直线BF2与椭圆的另一个交点为D，若tan∠F1BO=$\frac{3}{4}$，则直线CD的斜率为$\frac{12}{25}$．
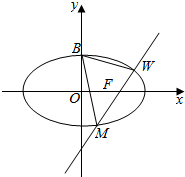已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{2}}{2}$，上顶点为B（0，1）．