题目内容
19.若复数z满足2z-$\overline{z}$=$\frac{2i-3}{i}$(i为虚数单位),则|z|=( )| A. | $\sqrt{5}$ | B. | 5 | C. | $\sqrt{13}$ | D. | 13 |
分析 设z=a+bi(a,b∈R),代入2z-$\overline{z}$=$\frac{2i-3}{i}$,利用复数代数形式的乘除运算化简后结合复数相等的条件得到a,b的值,则|z|可求.
解答 解:设z=a+bi(a,b∈R),则$\overline{z}=a-bi$,
代入2z-$\overline{z}$=$\frac{2i-3}{i}$,
得2(a+bi)-(a-bi)=a+3bi=$\frac{(2i-3)(-i)}{-{i}^{2}}=2+3i$,
∴a=2,b=1,
则|z|=$\sqrt{{a}^{2}+{b}^{2}}=\sqrt{5}$.
故选:A.
点评 本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
4.在△ABC中,已知sin(A-B)cosB+cos(A-B)sinB≥1,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
4.已知集合A={x|x≤1},B={y|y=x${\;}^{\frac{1}{2}}$,x∈($\frac{1}{4}$,1)},则A∩B=( )
| A. | (-∞,1) | B. | (-∞,1] | C. | ($\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1] |
9.函数f(x)=cos2x+6cos($\frac{π}{2}$-x)的最大值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
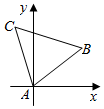 在平面直角坐标系中,定义两点A(xA,yA),B(xB,yB)间的“L-距离”为d(A-B)=|xA-xB|+|yA-yB|.现将边长为1的正三角形按如图所示方式放置,其中顶点A与坐标原点重合,记边AB所在的直线斜率为k(0≤k≤$\sqrt{3}$),则d(B-C)取得最大值时,边AB所在直线的斜率为2-$\sqrt{3}$.
在平面直角坐标系中,定义两点A(xA,yA),B(xB,yB)间的“L-距离”为d(A-B)=|xA-xB|+|yA-yB|.现将边长为1的正三角形按如图所示方式放置,其中顶点A与坐标原点重合,记边AB所在的直线斜率为k(0≤k≤$\sqrt{3}$),则d(B-C)取得最大值时,边AB所在直线的斜率为2-$\sqrt{3}$. 如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).
如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).