题目内容

判断f（x）=1-2x²在x∈[0，+∞）的单调性，并用定义证明．

函数f（x）=1-2x²在[0，+∞）上为单调减函数．其证明如下：
任取0≤x₁＜x₂，则f（x₂）-f（x₁）=1-2x₂²-1+2x₁²
=2x₁²-2x₂²=2（x₁-x₂）（x₁+x₂）
∵0≤x₁＜x₂，∴x₁-x₂＜0，x₁+x₂＞0
∴f（x₂）-f（x₁）＜0，即f（x₂）＜f（x₁）
故f（x）=1-2x²在[0，+∞）上为单调减函数．

练习册系列答案

开心练习课课练与单元检测系列答案

360全优测评系列答案

为了灿烂的明天系列答案

口算心算速算天天练江苏人民出版社系列答案

开心考卷单元测试卷系列答案

开心试卷期末冲刺100分系列答案

驿站新跨越系列答案

黄冈小状元培优周课堂系列答案

小学期中期末培优卷系列答案

双基同步导航训练系列答案

相关题目

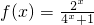已知f（x）是定义在R上的奇函数，对任意的x都有f（x+2）=f（x）成立，且当x∈（0，1）时f(x)=

．
（1）判断f（x）在（0，1）上的单调性，并加以证明；
（2）求f（x）在[-1，1]上的解析式；
（3）当关于x的方程f（x）-1=2λ在[-1，1]上有实数解时，求实数λ的取值范围，

已知函数f（x）=x²+

（x≠0）．
（1）判断f（x）的奇偶性，并说明理由；
（2）若f（1）=2，试判断f（x）在[2，+∞）上的单调性．

已知y=f（x）的定义域为R，且对任意的实数x，恒有等式2f（x）+f（-x）-3•2^sinx=0成立．
（1）试求f（x）的解析式；
（2）判断f（x）在[-

]的单调性，并用单调性定义予以证明；
（3）若f(x)=

，求满足条件的所有实数x的集合．

已知f（x）是定义在R上的奇函数，对任意的x都有f（x+2）=f（x）成立，且当x∈（0，1）时 $数学公式$ ．
（1）判断f（x）在（0，1）上的单调性，并加以证明；
（2）求f（x）在[-1，1]上的解析式；
（3）当关于x的方程f（x）-1=2λ在[-1，1]上有实数解时，求实数λ的取值范围，

已知f（x）是定义在R上的奇函数，对任意的x都有f（x+2）=f（x）成立，且当x∈（0，1）时f(x)=

．
（1）判断f（x）在（0，1）上的单调性，并加以证明；
（2）求f（x）在[-1，1]上的解析式；
（3）当关于x的方程f（x）-1=2λ在[-1，1]上有实数解时，求实数λ的取值范围，