f (x)=$\sqrt{{x}^{2}-2}$+$\sqrt{2-{x}^{2}}$ 的奇偶性是( )A．奇函数B．偶函数C．既奇又偶函数D．非奇非偶函数题目和参考答案——青夏教育精英家教网—

题目内容

4．f （x）=$\sqrt{{x}^{2}-2}$+$\sqrt{2-{x}^{2}}$ 的奇偶性是（　　）

A．

奇函数

B．

偶函数

C．

既奇又偶函数

D．

非奇非偶函数

分析由条件求得定义域为{x|x=±$\sqrt{2}$}，且满足f（x）=0，可得函数f（x）为即是奇函数又是偶函数．

解答解：$f（x）=\sqrt{{x^2}-2}+\sqrt{2-{x^2}}$的定义域为{x|x=±$\sqrt{2}$}，
且满足f（x）=0，故函数f（x）为即是奇函数又是偶函数，
故选：C．

点评本题主要考查函数的奇偶性的判断方法，求得f（x）=0是解题的关键，属于基础题．

练习册系列答案

名师点拨课时作业甘肃教育出版社系列答案

相关题目

15．

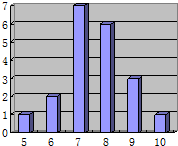某射击小组有20个人，教练根据他们某次射击的数据绘制成如图的统计图，则这组数据的众数和中位数分别是（　　）

16．已知a＞0，b＜0，则“a+b=0”是“a+b≥2ab”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

12．若函数$y=sin（{ωx+\frac{π}{4}}）$的图象与y轴距离最小的对称轴方程为$x=\frac{π}{6}$，则实数ω的值为$\frac{3}{2}$．

19．函数y=f（x-2）与y=-f（-x+2）图象关于点（2，0）对称．

9．若集合P={x|-1≤x＜5}，Q={x|x≥1}，则P∩Q等于（　　）

16．函数f（x）在（-∞，+∞）上是奇函数，当x＞0时f（x）=x（2x-3），则f（-1）=1．

13．$\underset{lim}{n→∞}$（$\frac{{n}^{3}-1}{3{n}^{2}+n}$-$\frac{{n}^{2}+1}{3n+4}$）=$\frac{1}{3}$．

12．下列式子能表示y关于x的函数的是（　　）

y²=2x²

试题分类