Question

1．实数x，y满足条件$\left\{\begin{array}{l}x+y-4≤0\\ x-2y+2≥0\\ x≥0\\ y≥0\end{array}\right.$，则${（{\frac{1}{2}}）^{x-y}}$的最大值为（　　）

• A． 1
• B． 2
• C． 4
• D． 9

Answer 1

分析 画出可行域’将目标函数变形得到z的几何意义，数形结合求出最大值即可．

解答 解；画出可行域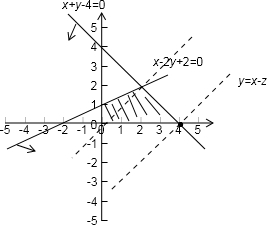

令z=x-y，变形为y=x-z，作出对应的直线，
将直线平移至点（4，0）时，直线纵截距最小，z最大，
将直线平移至点（0，1）时，直线纵截距最大，z最小，
将（0，1）代入z=x-y得到z的最小值为-1，
则${（{\frac{1}{2}}）^{x-y}}$的最大值是2，
故选：B．

点评 本题是线性规划问题．画出不等式组的可行域、将目标函数赋予几何意义、数形结合求出目标函数的最值．