Question

如图，船行前方的河道上有一座圆拱桥，在正常水位时，拱圈最高点距水面为9m，拱圈内水面宽22m．船顶部宽4m，船只在水面以上部分高6.5m时通行无阻．近日水位暴涨了2.7m，船已经不能通过桥洞了．船员必须加重船载，降低船身．试问船身必须降低多少米，才能顺利地通过桥洞？（精确到0.01m，参考数据QUOTE≈99.383）

Answer 1

考点：直线与圆的位置关系

专题：计算题,直线与圆

分析：建立坐标系，确定圆的方程，再令x=2，即可求得通过桥洞，船身至少应该降低多少．

解答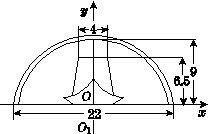： 解：以正常水位时河道中央O为原点，过点O垂直于水面的直线为y轴，
建立平面直角坐标系，如图所示．
设桥拱圆的圆心O₁（0，y₀），半径为r，则圆的方程为x²+（y-y₀）²=r²．
依题意得（r-9）²+11²=r²，解得r=

101

9

，y₀=-

20

9

．
圆的方程为x²+(y+

20

9

)2=(

101

9

)2．
当x=2时，y=

9877 -20

9

≈8.82．
8.82-6.5=2.32，即船身必须降低2.32米，才能顺利地通过桥洞．

点评：本题考查圆的标准方程，考查圆的方程的运用，正确建立坐标系是关键．